Companheiros venho mais uma vez solicitar a ajuda de vcs. A questão é a seguinte:
No plano cartesiano, a equação x² - 4xy - 5y² = 0 representa:
a) uma hipérbole
b) uma parábola
c) uma elipse
d) duas retas paralelas
e) duas retas concorrentes (resposta do gabarito)
Eu tentei ajuda nos livros de geometria analítica e nenhum exemplo parecido com a situação. Tentei desmenbrar em duas equações e não consegui.
Como faço para reconhecer que essa equação são duas retas concorrentes? Existe um método prático? Ou outro recurso? Agradeço quem puder ajudar.
.Mas no caso em questão ,podemos fatorar tal equação .Veja : ![x^2 -4xy -5y^2 = (x^2 -4xy -5y^2 ) + 0 = (x^2 -4xy -5y^2 ) + -xy +xy = [x^2 +xy ] + [-4xy -xy -5y^2] = x[x+y] -5y[x+y] = [x+y][x-5y] = 0 \implies \begin{cases} x+y = 0 \\ x -5y = 0 \end{cases}](/latexrender/pictures/e5a8d89c9037c59525246c9cd999bdb9.png "x^2 -4xy -5y^2 = (x^2 -4xy -5y^2 ) + 0 = (x^2 -4xy -5y^2 ) + -xy +xy = [x^2 +xy ] + [-4xy -xy -5y^2] = x[x+y] -5y[x+y] = [x+y][x-5y] = 0 \implies \begin{cases} x+y = 0 \\ x -5y = 0 \end{cases}")
.![(*) x^2-4xy-5y^2 = [x+y][x-5y] = 0](/latexrender/pictures/193b57cbfbc53f58939fe5fbc67d1159.png "(*) x^2-4xy-5y^2 = [x+y][x-5y] = 0")
, portanto 
ou 
.A equação
é a reunião das retas 
e 
(se é assim que podemos dizer ) .Para estudar a posição relativa entre as retas ,inicialmente podemos tomar a interseção entre elas ,isto é , resolver aquele sistema que já foi citado .Se 
podemos concluir que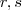 
são concorrentes ou paralelas coincidentes . Teremos estes dois casos a estudar .![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)