 por fernandocez » Qua Mai 08, 2013 18:48
por fernandocez » Qua Mai 08, 2013 18:48
Companheiros venho mais uma vez solicitar a ajuda de vcs. A questão é a seguinte:
No plano cartesiano, a equação x² - 4xy - 5y² = 0 representa:
a) uma hipérbole
b) uma parábola
c) uma elipse
d) duas retas paralelas
e) duas retas concorrentes (resposta do gabarito)
Eu tentei ajuda nos livros de geometria analítica e nenhum exemplo parecido com a situação. Tentei desmenbrar em duas equações e não consegui.
Como faço para reconhecer que essa equação são duas retas concorrentes? Existe um método prático? Ou outro recurso? Agradeço quem puder ajudar.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por e8group » Qua Mai 08, 2013 21:39
por e8group » Qua Mai 08, 2013 21:39
Se não me engano geralmente utilizamos mudança de coordenadas para eliminar o termo

.Mas no caso em questão ,podemos fatorar tal equação .Veja :
![x^2 -4xy -5y^2 = (x^2 -4xy -5y^2 ) + 0 = (x^2 -4xy -5y^2 ) + -xy +xy = [x^2 +xy ] + [-4xy -xy -5y^2] = x[x+y] -5y[x+y] = [x+y][x-5y] = 0 \implies \begin{cases} x+y = 0 \\ x -5y = 0 \end{cases} x^2 -4xy -5y^2 = (x^2 -4xy -5y^2 ) + 0 = (x^2 -4xy -5y^2 ) + -xy +xy = [x^2 +xy ] + [-4xy -xy -5y^2] = x[x+y] -5y[x+y] = [x+y][x-5y] = 0 \implies \begin{cases} x+y = 0 \\ x -5y = 0 \end{cases}](/latexrender/pictures/e5a8d89c9037c59525246c9cd999bdb9.png)
.
Tente observar se a interseção é diferente do vazio .Comente as dúvidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qua Mai 08, 2013 22:08
por e8group » Qua Mai 08, 2013 22:08
Pensando bem a última implicação não é verdadeira .Como vimos
![(*) x^2-4xy-5y^2 = [x+y][x-5y] = 0 (*) x^2-4xy-5y^2 = [x+y][x-5y] = 0](/latexrender/pictures/193b57cbfbc53f58939fe5fbc67d1159.png)
, portanto

ou

.A equação

é a reunião das retas

e

(se é assim que podemos dizer ) .Para estudar a posição relativa entre as retas ,inicialmente podemos tomar a interseção entre elas ,isto é , resolver aquele sistema que já foi citado .Se

podemos concluir que
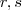
são concorrentes ou paralelas coincidentes . Teremos estes dois casos a estudar .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fernandocez » Sex Dez 20, 2013 09:54
por fernandocez » Sex Dez 20, 2013 09:54
Obrigado e feliz natal.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [GEOMETRIA ANALITICA] RETAS CONCORRENTES
por Patrick_GA » Qui Abr 23, 2015 10:52
- 0 Respostas
- 2136 Exibições
- Última mensagem por Patrick_GA

Qui Abr 23, 2015 10:52
Geometria Analítica
-
- Determinar se duas retas são concorrentes, paralelas...
por samra » Ter Mai 08, 2012 12:52
- 2 Respostas
- 5398 Exibições
- Última mensagem por samra

Ter Mai 08, 2012 22:23
Geometria Analítica
-
- [Geometria Plana] Circunferencia tangencida por duas retas
por stuartl » Dom Out 13, 2013 12:04
- 0 Respostas
- 1737 Exibições
- Última mensagem por stuartl

Dom Out 13, 2013 12:04
Geometria Plana
-
- Retas concorrentes
por marquinhoibvb » Qui Jun 05, 2008 22:39
- 1 Respostas
- 10650 Exibições
- Última mensagem por admin

Sex Jun 06, 2008 00:27
Geometria Analítica
-
- Retas Concorrentes
por lsergio_santos » Qui Jun 11, 2015 17:12
- 1 Respostas
- 2696 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:04
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .Mas no caso em questão ,podemos fatorar tal equação .Veja :
.Mas no caso em questão ,podemos fatorar tal equação .Veja : ![x^2 -4xy -5y^2 = (x^2 -4xy -5y^2 ) + 0 = (x^2 -4xy -5y^2 ) + -xy +xy = [x^2 +xy ] + [-4xy -xy -5y^2] = x[x+y] -5y[x+y] = [x+y][x-5y] = 0 \implies \begin{cases} x+y = 0 \\ x -5y = 0 \end{cases} x^2 -4xy -5y^2 = (x^2 -4xy -5y^2 ) + 0 = (x^2 -4xy -5y^2 ) + -xy +xy = [x^2 +xy ] + [-4xy -xy -5y^2] = x[x+y] -5y[x+y] = [x+y][x-5y] = 0 \implies \begin{cases} x+y = 0 \\ x -5y = 0 \end{cases}](/latexrender/pictures/e5a8d89c9037c59525246c9cd999bdb9.png) .
.![(*) x^2-4xy-5y^2 = [x+y][x-5y] = 0 (*) x^2-4xy-5y^2 = [x+y][x-5y] = 0](/latexrender/pictures/193b57cbfbc53f58939fe5fbc67d1159.png) , portanto
, portanto  ou
ou  .A equação
.A equação é a reunião das retas
é a reunião das retas  e
e  (se é assim que podemos dizer ) .Para estudar a posição relativa entre as retas ,inicialmente podemos tomar a interseção entre elas ,isto é , resolver aquele sistema que já foi citado .Se
(se é assim que podemos dizer ) .Para estudar a posição relativa entre as retas ,inicialmente podemos tomar a interseção entre elas ,isto é , resolver aquele sistema que já foi citado .Se  podemos concluir que
podemos concluir que 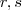 são concorrentes ou paralelas coincidentes . Teremos estes dois casos a estudar .
são concorrentes ou paralelas coincidentes . Teremos estes dois casos a estudar .
 .
.
 :
: