
Mudando a variável de integração para:
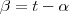

No exercício diz que
 . Queria que alguém me explicasse porquê, deve ser algo trivial mas está a passar-me ao lado...
. Queria que alguém me explicasse porquê, deve ser algo trivial mas está a passar-me ao lado...E já agora quais são as regras para a mudança de intervalo de integração com a mudança de variável?
Muito obrigado


 , então, a derivada dos dois membros da igualdade será
, então, a derivada dos dois membros da igualdade será 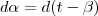
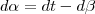 , como t é considerado constante, o valor
, como t é considerado constante, o valor  é zero, então ficará:
é zero, então ficará: , pois eu passei apenas
, pois eu passei apenas 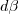 para o 1º membro
para o 1º membro

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)