 por Skyliner » Qua Nov 25, 2009 23:02
por Skyliner » Qua Nov 25, 2009 23:02
Boas, estou com uma dúvida num exercício que está resolvido, por isso vou postar só a parte que tenho dúvida e que interessa!

Mudando a variável de integração para:
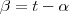

No exercício diz que

. Queria que alguém me explicasse porquê, deve ser algo trivial mas está a passar-me ao lado...
E já agora quais são as regras para a mudança de intervalo de integração com a mudança de variável?
Muito obrigado
-
Skyliner
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Nov 25, 2009 22:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por thadeu » Qui Nov 26, 2009 01:05
por thadeu » Qui Nov 26, 2009 01:05
skiliner, se foi falado que

, então, a derivada dos dois membros da igualdade será
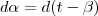
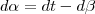
, como t é considerado constante, o valor

é zero, então ficará:

, pois eu passei apenas
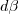
para o 1º membro
-
thadeu
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Out 19, 2009 14:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Skyliner » Qui Nov 26, 2009 01:08
por Skyliner » Qui Nov 26, 2009 01:08
como eu tinha dito, era trivial, só que já estou com umas horas de estudo e há coisas que passam ao lado

muito obrigado.
-
Skyliner
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Nov 25, 2009 22:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Mudança de Variável
por DanielFerreira » Dom Abr 22, 2012 13:58
- 2 Respostas
- 1603 Exibições
- Última mensagem por DanielFerreira

Ter Abr 24, 2012 20:31
Cálculo: Limites, Derivadas e Integrais
-
- Mudança de Variável
 por DanielFerreira » Dom Abr 29, 2012 21:06
por DanielFerreira » Dom Abr 29, 2012 21:06
- 3 Respostas
- 1870 Exibições
- Última mensagem por LuizAquino

Ter Mai 01, 2012 15:56
Cálculo: Limites, Derivadas e Integrais
-
- Dúvidas em mudança de variável
por pam_nivens » Sáb Nov 28, 2009 21:26
- 2 Respostas
- 5457 Exibições
- Última mensagem por pam_nivens

Dom Nov 29, 2009 01:37
Cálculo: Limites, Derivadas e Integrais
-
- Mudança de variavel na integral
por matmatco » Ter Abr 23, 2013 22:29
- 0 Respostas
- 1119 Exibições
- Última mensagem por matmatco

Ter Abr 23, 2013 22:29
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Mudança de variável
por VFernandes » Ter Jan 03, 2012 23:47
- 2 Respostas
- 2138 Exibições
- Última mensagem por VFernandes

Qui Jan 05, 2012 23:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

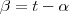

 . Queria que alguém me explicasse porquê, deve ser algo trivial mas está a passar-me ao lado...
. Queria que alguém me explicasse porquê, deve ser algo trivial mas está a passar-me ao lado...

 , então, a derivada dos dois membros da igualdade será
, então, a derivada dos dois membros da igualdade será 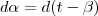
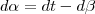 , como t é considerado constante, o valor
, como t é considerado constante, o valor  é zero, então ficará:
é zero, então ficará: , pois eu passei apenas
, pois eu passei apenas 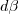 para o 1º membro
para o 1º membro
