Sejam a, b e c números reais não nulos, tais que a + b + c = 0. Determine os possíveis valores de
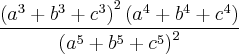
a)

b)
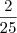
c)

d)

e)


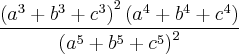

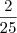




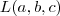 )só pode ser constante ,pois o conjunto que goza da propriedade
)só pode ser constante ,pois o conjunto que goza da propriedade  é não-enumerável .Agora convenhamos,caso
é não-enumerável .Agora convenhamos,caso 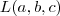 não fosse constante não seria uma tarefa simples obter a,b,c particulares tais que
não fosse constante não seria uma tarefa simples obter a,b,c particulares tais que 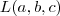 coincide com uma das alternativas ,o que acha ?
coincide com uma das alternativas ,o que acha ? 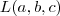 é constante vamos desenvolver esta expressão .
é constante vamos desenvolver esta expressão . 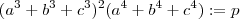

 (1) ,podemos obter algumas relações :
(1) ,podemos obter algumas relações : ![0= 0^2=(a+b+c)^2 = a^2+b^2+c^2 + 2(ab +ac +bc) = a^2+b^2+c^2 + 2(a[b+c] +bc) 0= 0^2=(a+b+c)^2 = a^2+b^2+c^2 + 2(ab +ac +bc) = a^2+b^2+c^2 + 2(a[b+c] +bc)](/latexrender/pictures/055937247bc3c96362c7f2acacfb93ea.png) ,logo
,logo 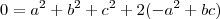 e assim ,
e assim ,  (2) .
(2) . e preservar as estruturas algébricas ,obtendo
e preservar as estruturas algébricas ,obtendo ![(a^2+b^2+c^2 )^2 =a^4+b^4+c^4 + 2(a^2[b^2+c^2] +b^2c^2) = 4(a^2-bc)^2 (a^2+b^2+c^2 )^2 =a^4+b^4+c^4 + 2(a^2[b^2+c^2] +b^2c^2) = 4(a^2-bc)^2](/latexrender/pictures/834052e412540b91949f192883079f6d.png) e daí ,
e daí , ![\boxed{a^4+b^4+c^4 = 4(a^2-bc)^2 - 2(a^2[b^2+c^2] +b^2c^2)} \boxed{a^4+b^4+c^4 = 4(a^2-bc)^2 - 2(a^2[b^2+c^2] +b^2c^2)}](/latexrender/pictures/6725950c1dda96a4079412b0385e47f8.png) (3) .
(3) .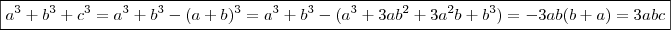 (4) e
(4) e  (5) .
(5) . 

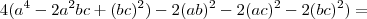

![\ 4a^4 + 8a^2b[a+b] + 2(b[a+b])^2 -2(ab)^2 -2(a[a+b])^2 = \ 4a^4 + 8a^2b[a+b] + 2(b[a+b])^2 -2(ab)^2 -2(a[a+b])^2 =](/latexrender/pictures/ea1ecffe3bdf0134e83d9e888d7513d8.png)

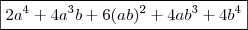 (5)
(5)![0 = (a+b+c)(a^4+b^4+c^4) = \hdots = 3(a^5+b^5+c^5) + (a^3+b^3+c^3)(3[ab +bc +ac] -[a^2+b^2+c^2]) 0 = (a+b+c)(a^4+b^4+c^4) = \hdots = 3(a^5+b^5+c^5) + (a^3+b^3+c^3)(3[ab +bc +ac] -[a^2+b^2+c^2])](/latexrender/pictures/99a910bd76d0fe9272637bf0aef0cc9b.png)
 por
por  e
e  por
por 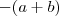 (somente em algumas parcelas ,não todas !) obtemos
(somente em algumas parcelas ,não todas !) obtemos ![0 = 3(a^5+b^5+c^5) + (a^3+b^3+c^3)(3[ab -b(a+b) -a(a+b)] -2(a^2+b(a+b)) =
3(a^5+b^5+c^5) + (a^3+b^3+c^3)(3[-b^2- a^2 -ab] -2a^2 -2ab -2b^2) =
3(a^5+b^5+c^5) -5(a^3+b^3+c^3)(a^2 +b^2 +ab) 0 = 3(a^5+b^5+c^5) + (a^3+b^3+c^3)(3[ab -b(a+b) -a(a+b)] -2(a^2+b(a+b)) =
3(a^5+b^5+c^5) + (a^3+b^3+c^3)(3[-b^2- a^2 -ab] -2a^2 -2ab -2b^2) =
3(a^5+b^5+c^5) -5(a^3+b^3+c^3)(a^2 +b^2 +ab)](/latexrender/pictures/129a434b2b3420da546b8fc6e523b767.png)
 e portanto
e portanto 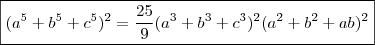 (6) , ou se preferir ,expandindo
(6) , ou se preferir ,expandindo  que multiplicada por
que multiplicada por  nos dá exatamente (5) ,então concluímos que
nos dá exatamente (5) ,então concluímos que  . De (5) ,resulta :
. De (5) ,resulta :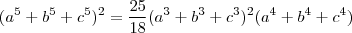 (7) .
(7) .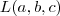 é constante e é igual a
é constante e é igual a  .
. 
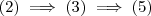 e por aí vai ...
e por aí vai ...
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



