Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por barbaramattos » Seg Dez 16, 2013 01:27
por barbaramattos » Seg Dez 16, 2013 01:27
O lucro obtido por um comerciante na venda de determinado produto é dado , em reais, pela função L(x)= -1/10x²+ 15x, sendo x o número de unidades vendidas e o menor que x menor que 150.
Se L(m) é o lucro máximo que comerciante tem condições de obter, pode-se afirmar que log( l(m)/3m) é igual a:
a) 1+2log2
b) 2log2+log5
c) 2-log5
d) 1-2log2
e) 1-2log5
-
barbaramattos
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Dez 16, 2013 00:04
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por Russman » Seg Dez 16, 2013 18:31
por Russman » Seg Dez 16, 2013 18:31
O enunciado está confuso, mas acredito que você deva calcular o lucro máximo obtido na venda das unidades. Para isto, repare que a função lucro é quadrática em x( ao menos é o que parece) e você deve ter tido contato com uma fórmula que calcule o "ponto de vértice" da forma quadrática da função graficada. Pois o faça. Uma vez calculado m e L(m) faça a operação indicada e aplique o logaritmo.
OBS: TENTE fazer a questão e poste seus resusltados bem como suas possíveis dúvidas em algum passo.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por barbaramattos » Seg Dez 16, 2013 21:22
por barbaramattos » Seg Dez 16, 2013 21:22
desculpe-me por não postar explicações ditas iniciais. Eu não sei fazer esta questão por causa que não vi ainda uma semelhante ou igual a essa.
Essa é a minha dificuldade.
-
barbaramattos
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Dez 16, 2013 00:04
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por barbaramattos » Seg Dez 16, 2013 21:48
por barbaramattos » Seg Dez 16, 2013 21:48
desculpe-me por não postar as informações ditas iniciais. O fato da questão não apresentar resolução, seria pelo seguinte problema: ainda não encontrei alguma questão parecida ou semelhante, portanto, impossibilita-me fazê-la. Por gentileza, fico agradecida se o senhor a resolvesse ou mostrasse uma semelhante para mim, que auxiliasse em meus estudos. Pense: numa sala de aula quando uma aluna não sabe resolver uma questão ela recorre a um professor ou a alguém que sabe mais que ela,contudo, caso soubesse resolvê-la não precisaria de ninguém e nem de ajuda cibernética de voluntariado.
Ajudem-me, por favor, aqueles de boa vontade.
-
barbaramattos
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Dez 16, 2013 00:04
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por Russman » Seg Dez 16, 2013 22:21
por Russman » Seg Dez 16, 2013 22:21
MInha intenção não foi parecer estar de má vontade. É recorrente alunos buscando resoluções completas para trabalhos e afins. Mas, ok. Você me pareceu interessada.
Uma função do tipo
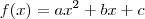
possui um ponto de extremo em
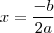
. Isto é, aplicando
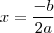
em

você calcula-rá o seu maior ou menor valor. Se

então o ponto é de mínimo e se
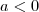
o ponto é de máximo. Naturalmente, calculando
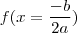
você chegará em
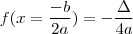
(onde este delta é o mesmo da fórmula de resolução de equações de 2º grau) que é o maior ou menor valor atingido pela função.
Como a sua função é

o ponto extremo será de máximo, pois

. Ele ocorre em
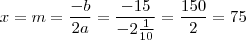
com valor
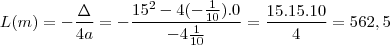
Agora, o exercicio manda fazer
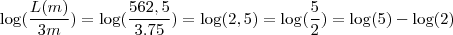
.
Basta aplicar as propriedade do logaritmo do quociente para chegar na resposta q eu escrevi. Porém, esse valor não está presente na questão. Ou eu calculei algum numero errado ou deve haver outro engano.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por barbaramattos » Seg Dez 16, 2013 23:07
por barbaramattos » Seg Dez 16, 2013 23:07
obrigada
-
barbaramattos
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Dez 16, 2013 00:04
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2569 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1846 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- Logaritmo
por JailsonJr » Sex Mai 21, 2010 05:11
- 3 Respostas
- 2726 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:33
Logaritmos
-
- Logaritmo (UF-CE)
por JailsonJr » Sáb Mai 22, 2010 04:56
- 6 Respostas
- 5262 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:32
Logaritmos
-
- Logaritmo
por nan_henrique » Sex Jul 09, 2010 18:38
- 1 Respostas
- 2276 Exibições
- Última mensagem por Elcioschin

Sex Jul 09, 2010 19:42
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



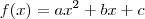 possui um ponto de extremo em
possui um ponto de extremo em 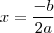 . Isto é, aplicando
. Isto é, aplicando  você calcula-rá o seu maior ou menor valor. Se
você calcula-rá o seu maior ou menor valor. Se  então o ponto é de mínimo e se
então o ponto é de mínimo e se 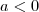 o ponto é de máximo. Naturalmente, calculando
o ponto é de máximo. Naturalmente, calculando 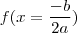 você chegará em
você chegará em 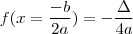 (onde este delta é o mesmo da fórmula de resolução de equações de 2º grau) que é o maior ou menor valor atingido pela função.
(onde este delta é o mesmo da fórmula de resolução de equações de 2º grau) que é o maior ou menor valor atingido pela função. o ponto extremo será de máximo, pois
o ponto extremo será de máximo, pois  . Ele ocorre em
. Ele ocorre em 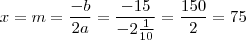
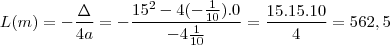
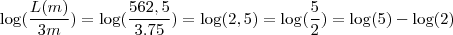 .
.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.