


 e os pontos
e os pontos  .Encontre um ponto pertencendo à reta
.Encontre um ponto pertencendo à reta  tal que a distância deste ponto ao ponto
tal que a distância deste ponto ao ponto  seja a mesma ao ponto
seja a mesma ao ponto . Em resumo , deve determinar
. Em resumo , deve determinar  .
.
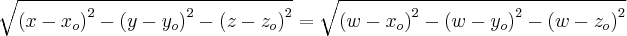

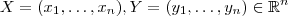 e dada por
e dada por 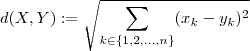 . Por exemplo em
. Por exemplo em  .
. 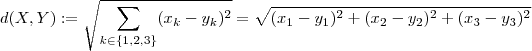 e não a fórmula que você apresentou .
e não a fórmula que você apresentou . 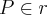 então para algum
então para algum  real ,tem-se
real ,tem-se 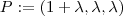 . Em particular devemos escolher
. Em particular devemos escolher  tal que
tal que 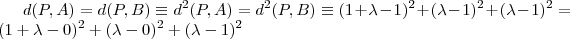 .
. 

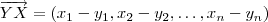 . Calculando o produto escalar
. Calculando o produto escalar  em termos das componentes destes vetores vamos obter
em termos das componentes destes vetores vamos obter 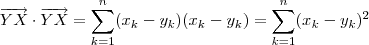 . A raiz quadrada desta expressão forne a distância de
. A raiz quadrada desta expressão forne a distância de  a
a  .
. 

 e um ponto
e um ponto  ?
? 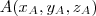 e
e 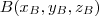 o vetor que liga estes pontos é escrito como
o vetor que liga estes pontos é escrito como  e suas componentes são as diferenças das coordenadas respectivas de cada ponto. Isto é,
e suas componentes são as diferenças das coordenadas respectivas de cada ponto. Isto é,  .
. 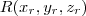 da reta
da reta  são todos escritos da forma
são todos escritos da forma 

 .
. ao ponto
ao ponto  é
é
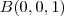 é
é
 e , com a solução, poderá calcular o respectivo ponto da reta que dista o mesmo de
e , com a solução, poderá calcular o respectivo ponto da reta que dista o mesmo de  e
e  .
. a solução.
a solução.

Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes