 por rochadapesada » Sáb Dez 14, 2013 20:46
por rochadapesada » Sáb Dez 14, 2013 20:46
Como saber se 1 vetor apenas é LD ou LI? Eu sei que quando 1 vetor é LD quando vetor=0 e é LI, quando o vetor é diferente de 0... Mas como provar isso?
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Sáb Dez 14, 2013 22:00
por e8group » Sáb Dez 14, 2013 22:00
Qualquer conjunto que contém apenas um vetor é L.I. desde que este vetor não seja o nulo e caso contrário L.D . Lembre-se que dizemos um conjunto
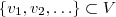
(V espaço vetorial) é L.I. quando a combinação linear nula

é verdadeira somente quando todos escalares
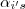
são iguais a zero .(Onde

é o vetor nulo do espaço vetorial V ) . Se Caso pelo menos um desses escalares for diferente de zero dizemos que
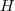
L.D.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por rochadapesada » Sáb Dez 14, 2013 22:29
por rochadapesada » Sáb Dez 14, 2013 22:29
estou enganado, mas você me respondeu com álgebra linear? Eu não estou dando álgebra ainda :/
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Sáb Dez 14, 2013 22:59
por e8group » Sáb Dez 14, 2013 22:59
Sim ,respondi utilizando A.L.. Foi em G.A. que viu este conceito ? Caso seja, recomendo uma leitura no capítulo 6 do livro - Um tratamento vetorial por Ivan de Camargo , Paulo Boulos . Lá encontrará as definições e as proposições . EM G.A. nos livros em geral , define-se uma sequência (v) de vetores L.I. se v \neq 0 e (v) L.D. se v = 0 .Não há nada que provar , és a definição .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por rochadapesada » Sáb Dez 14, 2013 23:09
por rochadapesada » Sáb Dez 14, 2013 23:09
então, foi por ele que peguei e ele pede para mostrar, veja ai e como é em geometria analítica, ai complica:
- Anexos
-

-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Sáb Dez 14, 2013 23:31
por e8group » Sáb Dez 14, 2013 23:31
Se
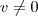
então por definição
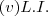
e se

(vetor nulo ) ,

. Isto foi definido não há nada que demostrar .É só isso ? Ou algo mais ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por rochadapesada » Sáb Dez 14, 2013 23:44
por rochadapesada » Sáb Dez 14, 2013 23:44
se puder responder minha outra pergunta que está no outro tópico eu fico agradecido pakas =DD... Neste tópico é só isso Vlwzaço =DD
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- como saber se o sistema é possível ..
por willwgo » Qua Abr 03, 2013 19:13
- 1 Respostas
- 1895 Exibições
- Última mensagem por Banach

Sex Abr 05, 2013 08:42
Sistemas de Equações
-
- Como saber se duas funções se interceptam ou não.
por marlonsouza23 » Sex Set 21, 2012 18:48
- 3 Respostas
- 12396 Exibições
- Última mensagem por fraol

Sáb Set 22, 2012 16:04
Funções
-
- Gostaria de saber, como surgiu esta formula.
por bencz » Qui Jul 14, 2011 00:27
- 1 Respostas
- 1853 Exibições
- Última mensagem por Molina

Dom Jul 17, 2011 15:10
Geometria Analítica
-
- Gostaria de saber como calcular o seguinte limite
por felipe_08 » Qui Abr 23, 2015 17:36
- 2 Respostas
- 2578 Exibições
- Última mensagem por felipe_08

Qui Abr 23, 2015 22:51
Cálculo: Limites, Derivadas e Integrais
-
- problema , queria saber como resolver e a explicaçao
por ricks » Ter Mai 05, 2015 22:23
- 1 Respostas
- 2580 Exibições
- Última mensagem por adauto martins

Qua Mai 06, 2015 13:20
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



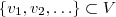 (V espaço vetorial) é L.I. quando a combinação linear nula
(V espaço vetorial) é L.I. quando a combinação linear nula  é verdadeira somente quando todos escalares
é verdadeira somente quando todos escalares 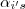 são iguais a zero .(Onde
são iguais a zero .(Onde  é o vetor nulo do espaço vetorial V ) . Se Caso pelo menos um desses escalares for diferente de zero dizemos que
é o vetor nulo do espaço vetorial V ) . Se Caso pelo menos um desses escalares for diferente de zero dizemos que 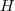 L.D.
L.D.



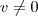 então por definição
então por definição 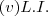 e se
e se  (vetor nulo ) ,
(vetor nulo ) ,  . Isto foi definido não há nada que demostrar .É só isso ? Ou algo mais ?
. Isto foi definido não há nada que demostrar .É só isso ? Ou algo mais ?


 .
.
 :
: