Resolver o sistema de equações para x>0 e y>0 e m*n>0


......não faço idéia de como fica isso.. o pouco que eu fiz, foi..

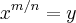
..


...
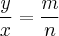
...
Alguém desenrola essa pra mim?
Grato!!^^




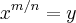


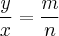

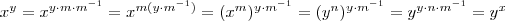 e assim ,
e assim , 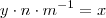 (1)
(1) 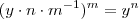 sse
sse ![y^m \cdot [n\cdot m^{-1}]^m = y^n y^m \cdot [n\cdot m^{-1}]^m = y^n](/latexrender/pictures/c3602f860fd1c62e12d8fe7cc2017b55.png) sse
sse 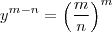 (2) .
(2) .  segue-se que qualquer
segue-se que qualquer 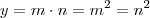 satisfaz
satisfaz  , bem como satisfaz
, bem como satisfaz 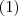 . Agora suponha
. Agora suponha 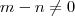 .Neste caso ,
.Neste caso ,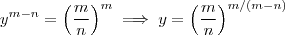 (3) e por (1) obtemos que
(3) e por (1) obtemos que 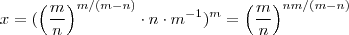 (4)
(4)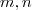 em
em  tais que
tais que 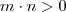 e
e  obteremos soluções para
obteremos soluções para  e
e  dada por (4) e (3) respectivamente e caso
dada por (4) e (3) respectivamente e caso  , as soluções para
, as soluções para 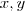 são dadas por
são dadas por 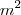 .
.

BrunoLima escreveu:Boa noite santhiago, muito obrigado pela sua explicação consegui, com muita dificuldade compreender, mas você poderia mostrar melhor, a parte que vc diz ''(3) e por 1 obtemos" ?? pq ficou tudo elevado a m?
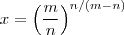 e
e  no sistema :
no sistema : ![x^y= \left[ \left(\frac{m}{n}\right)^{n/(m-n)} \right]^{\left(\frac{m}{n}\right)^{m/(m-n)}} x^y= \left[ \left(\frac{m}{n}\right)^{n/(m-n)} \right]^{\left(\frac{m}{n}\right)^{m/(m-n)}}](/latexrender/pictures/b4a3be406c6df89666f73cd14ffe6311.png)
![y^x = \left[ \left(\frac{m}{n}\right)^{m/(m-n)} \right]^{\left(\frac{m}{n}\right)^{n/(m-n)}} y^x = \left[ \left(\frac{m}{n}\right)^{m/(m-n)} \right]^{\left(\frac{m}{n}\right)^{n/(m-n)}}](/latexrender/pictures/de1db756dcefa00686be60028a829d8f.png) .
.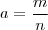 e
e 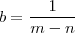 , desta forma
, desta forma 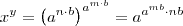
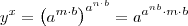
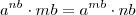
 ou ainda
ou ainda  que é equivalente a
que é equivalente a 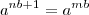 e novamente devemos impor que
e novamente devemos impor que 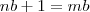 e assim
e assim 
 ,logo
,logo  OK! ,isto significa a primeira equação do sistema é satisfeita para todo
OK! ,isto significa a primeira equação do sistema é satisfeita para todo  e
e  reais distintos tais que
reais distintos tais que 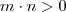 e
e  dependendo
dependendo 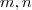 ( conforme já vimos que são eles ) .
( conforme já vimos que são eles ) .![x^m = \left[ \left(\frac{m}{n}\right)^{n/(m-n)}\right]^m = \left(\frac{m}{n}\right)^{nm/(m-n)} x^m = \left[ \left(\frac{m}{n}\right)^{n/(m-n)}\right]^m = \left(\frac{m}{n}\right)^{nm/(m-n)}](/latexrender/pictures/f94815b8315d97eb31b404d32b5e07e1.png) e
e ![y^n = \left[ \left(\frac{m}{n}\right)^{m/(m-n)}\right]^n = \left(\frac{m}{n}\right)^{nm/(m-n)} y^n = \left[ \left(\frac{m}{n}\right)^{m/(m-n)}\right]^n = \left(\frac{m}{n}\right)^{nm/(m-n)}](/latexrender/pictures/f5fe14d5c7bd8ff7fce5894ac28884b5.png)
 e
e  reais distintos tais que
reais distintos tais que 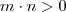 e
e  dependendo
dependendo 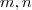 .
. então
então  ,e
,e  não dependem da escolha de
não dependem da escolha de 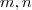 .
. 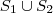 onde
onde 


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: