A função de Euler verifica os coprimos menores que o número dado então deveria ser igual 12:
{1,2,4,5,8,10,11,13,16,17,19,20} são coprimos de 21.
Pelo que vi na fórmula aqui
http://en.wikipedia.org/wiki/Euler%27s_totient_function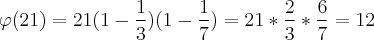
Os coprimos de 22 são:{1,3,5,7,9,11,13,15,17,19,21}, são 11
Os coprimos de 23 são:{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22}(visto que 23 é primo), mas aqui eu tenho 22
Os coprimos de 25 são:{1,2,3,4,6,7,8,9,11,12,13,14,16,17,18,19,21,22,23,24}, mas aqui eu tenho 20

Por esse gráfico aqui seria 23 , mas aí teríamos 22 e não 21... O 46 também tem 22 não é? Acho que não tem um número com essa propriedade
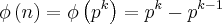
 , temos
, temos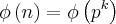 e
e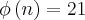

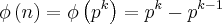
 , temos
, temos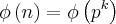 e
e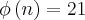

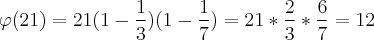








 , avisa que eu resolvo.
, avisa que eu resolvo.

