fiz assim,
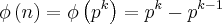
temos que para qualquer numero primo p,
 , temos
, temos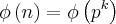 e
e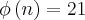
21= p-1
p = 22
mas esse resultado nao deve estar correto, alguém me ajuda?

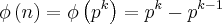
 , temos
, temos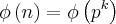 e
e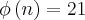

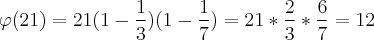






Voltar para Teoria dos Números
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

