duvida parabola

por **CarolMarques** » Seg Mai 07, 2012 20:37

O cabo de uma ponte suspensa tem a forma de uma parabola quando a carga é uniformemente distribuída na horizontal.A distância entre duas colunas é 150 m , os pontos de suporte do cabo nas colunas estão 22m acima da pista e o ponto mais baixo do cabo está 7 m da pista.Ache a distância vertical do cabo a um ponto na pista a 15 m do pé de uma coluna.

Eu não consigo montar a figura.A questão vem só com enunciado sem figura.Obrigada

por **LuizAquino** » Seg Mai 07, 2012 21:46

CarolMarques escreveu:O cabo de uma ponte suspensa tem a forma de uma parabola quando a carga é uniformemente distribuída na horizontal.A distância entre duas colunas é 150 m , os pontos de suporte do cabo nas colunas estão 22m acima da pista e o ponto mais baixo do cabo está 7 m da pista. Ache a distância vertical do cabo a um ponto na pista a 15 m do pé de uma coluna.

CarolMarques escreveu:Eu não consigo montar a figura. A questão vem só com enunciado sem figura.

A figura abaixo ilustra o exercício. O objetivo é determinar a distância h. Tente resolvê-lo agora.

: figura1.png (5.18 KiB) Exibido 9016 vezes

por **CarolMarques** » Seg Mai 07, 2012 22:48

Eu não consigo identificar o p.p=7?

por **LuizAquino** » Ter Mai 08, 2012 11:11

CarolMarques escreveu:Eu não consigo identificar o p.p=7?

Primeiro você precisa escolher um sistema de eixos conveniente. Por exemplo, vide a figura abaixo.

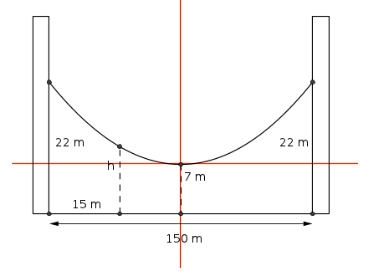
: figura.png (7.2 KiB) Exibido 9004 vezes

No sistema de eixos em destaque, a equação da parábola é $y = \frac{1}{4p}x^2$ .

Nesse sistema, para x = 75 temos que y = 22 - 7 = 15. Ou seja, essa parábola passa pelo ponto (75, 15).

Agora tente continuar o exercício.

por **CarolMarques** » Qui Mai 10, 2012 19:41

Consegui resolver!Obrigada!

por **Eriverton** » Sáb Jun 16, 2012 22:36

Quanto deu a resposta desta questão?

por **LuizAquino** » Dom Jun 17, 2012 09:48

Eriverton escreveu:Quanto deu a resposta desta questão?

A reposta é h = 83/5 m.

por **Eriverton** » Dom Jun 17, 2012 15:46

como faço para chegar a essa resposta?

por **Eriverton** » Dom Jun 17, 2012 18:12

chegueiii a essa resposta. VLW

por **Nhsouza1992** » Sáb Nov 30, 2013 20:47

Gente, voces poderiam me ajudar a resolver este exercício? Muito obrigado!

por **LuizAquino** » Dom Dez 01, 2013 07:59

Nhsouza1992 escreveu:Gente, voces poderiam me ajudar a resolver este exercício? Muito obrigado!

Tente seguir os passos:

Passo 1) Substitua o ponto (75, 15) na equação da parábola. Com isso, você descobrirá o valor de p.

Passo 2) Na equação da parábola, calcule o valor de y considerando que x = 60 (ou seja, x = (150/2) - 15).

Passo 3) Calcule o valor de h observando que h = 7 + y (sendo y o valor calculado no Passo 2)).

Se você não conseguir finalizar o exercício, poste aqui até onde você chegou com esses passos.

por **Nhsouza1992** » Dom Dez 01, 2013 19:55

LuizAquino escreveu:
Nhsouza1992 escreveu:Gente, voces poderiam me ajudar a resolver este exercício? Muito obrigado!

Tente seguir os passos:

Passo 1) Substitua o ponto (75, 15) na equação da parábola. Com isso, você descobrirá o valor de p.

Passo 2) Na equação da parábola, calcule o valor de y considerando que x = 60 (ou seja, x = (150/2) - 15).

Passo 3) Calcule o valor de h observando que h = 7 + y (sendo y o valor calculado no Passo 2)).

Se você não conseguir finalizar o exercício, poste aqui até onde você chegou com esses passos.