É o seguinte, sei que
 ou
ou  quando
quando  é verdade quando
é verdade quando 
Mas não consigo entender. Por exemplo:
Dada a função
 , prove pela definição formal que
, prove pela definição formal que  .
.


Ok, descobri isso. E agora? Que relação eu faço para provar que o limite existe por definição?
Por exemplo, neste mesmo caso, como eu posso provar, por definição, que:
 quando
quando  ?
?Sei que mudaria para:

E
 quando
quando  ?
?Sei que mudaria para:

E se eu não tiver um
 ? Como fica?
? Como fica?Por exemplo: Prove que a função
 não possui limite quando
não possui limite quando 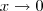 .
.

O que isso significa?
Desculpe pelo número de perguntas, porém a questão aqui é a explicação da relação entre
 , que até agora eu não entendi. As funções supracitadas são apenas exemplos para referenciar minhas dúvidas.
, que até agora eu não entendi. As funções supracitadas são apenas exemplos para referenciar minhas dúvidas.Obrigado pela paciência rs!


 quando
quando  tende a
tende a  é o número real
é o número real  .Tente adaptar a
.Tente adaptar a  e as demais questões em que
e as demais questões em que  é polinômio de grau 1 .
é polinômio de grau 1 . dado obteremos um
dado obteremos um  (dependendo da escolha de
(dependendo da escolha de  ) tal que para todo
) tal que para todo 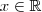 , se
, se  então
então  .
.  . Desta forma ,tomando-se
. Desta forma ,tomando-se  ,obtemos
,obtemos  , tal que se
, tal que se  então
então  .
. 
 . Uma operação desta não seria
. Uma operação desta não seria  ? Então por que
? Então por que  ?
? ?
? (mesmo ainda sem saber o porquê).
(mesmo ainda sem saber o porquê). então
então 
 , em seguida? O
, em seguida? O 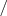 tem o papel de
tem o papel de  ou de divisão?
ou de divisão? . Quando fazemos todas as operações, não chegamos no resultado que
. Quando fazemos todas as operações, não chegamos no resultado que  ? (agora tô usando minha hipótese apontada logo acima)
? (agora tô usando minha hipótese apontada logo acima) . Além disso o simbolo
. Além disso o simbolo  para algum
para algum  ,sendo esta relação verdadeira então necessariamente ,
,sendo esta relação verdadeira então necessariamente , . Mas
. Mas  ,então
,então  . Ora , a expressão
. Ora , a expressão  é exatamente
é exatamente  ,desta forma
,desta forma  .
. ,qual a sua opinião ?
,qual a sua opinião ? , vamos provar que
, vamos provar que 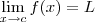 .
.

 ) acho que está meio errado rs. É isto mesmo?
) acho que está meio errado rs. É isto mesmo?



 .Suponhamos
.Suponhamos  mas ela está definida na vizinhança de
mas ela está definida na vizinhança de 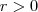 o quanto pequeno queremos ,
o quanto pequeno queremos ,  .Prosseguindo ...
.Prosseguindo ...  de números reais em
de números reais em  convergente para
convergente para 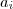 ao número
ao número  o quanto pequeno se queira ) que
o quanto pequeno se queira ) que  desde que
desde que  ou de forma equivalente
ou de forma equivalente  desde que
desde que  .
.  por
por  por
por  e
e  então
então  . Adaptando-se :
. Adaptando-se : e
e  então
então  e isto por sua vez implica
e isto por sua vez implica  .
. .
.