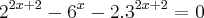
Então galera editando aqui.. eu dividi tudo por 6^x aí ficou
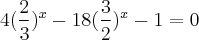
fazendo (2/3)^x = y eu econtrei a seguinte equação do segundo grau
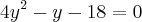
Ráizes= 9/4 e -2
-2 >> não convém 9/4 = (2/3)^x x=-2
Então galera eu consegui chegar a resposta do gabarito pois vi uma resolução parecida em um fórum e decidi tentar, como eu sou novo no fórum não sei muito bem o que fazer... se algum moderador quiser excluir tudo bem, se não, a questão está aí para quem estiver procurando, ou para alguém opinar uma resolução diferente..


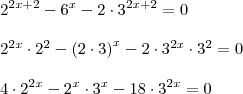
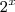 e
e  respectivamente por
respectivamente por  e
e  , onde
, onde