 por amigao » Seg Nov 25, 2013 18:14
por amigao » Seg Nov 25, 2013 18:14
Como faz esse limite, pela minha resolução seria Não existe, mas wolframalpha fala que seria 0. Me ajuda por favor?
- Anexos
-

- MSP33251de5ic0ba75b734400001c4g340ggc4881dd.gif (897 Bytes) Exibido 3282 vezes
-
amigao
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Mai 11, 2013 11:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Seg Nov 25, 2013 19:03
por e8group » Seg Nov 25, 2013 19:03
Repare que
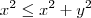
,isto por sua vez implica
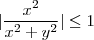
desde que

.Assim segue a função de duas variáveis definida pela expressão entre módulo é limitada por

.Aplicando propriedades de limite obterá o resultado desejado.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por amigao » Seg Nov 25, 2013 19:45
por amigao » Seg Nov 25, 2013 19:45
santhiago escreveu:Repare que
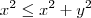
,isto por sua vez implica
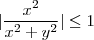
desde que

.Assim segue a função de duas variáveis definida pela expressão entre módulo é limitada por

.Aplicando propriedades de limite obterá o resultado desejado.
eu não entendi porque
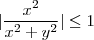
se a função tem denominador
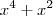
-
amigao
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Mai 11, 2013 11:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Seg Nov 25, 2013 20:17
por e8group » Seg Nov 25, 2013 20:17
Tem razão . Falta de atenção minha .Neste caso é possível ver que o limite não existe ,experimente aproximar do ponto
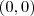
pela reta

e pela parábola

. Passando ao limite com

obterá dois resultados resultados distintos .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por amigao » Ter Nov 26, 2013 19:36
por amigao » Ter Nov 26, 2013 19:36
Consegui, muito obrigado pela ajuda
-
amigao
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Mai 11, 2013 11:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Limite de duas variáveis
por hygorvv » Dom Jun 30, 2013 09:31
- 1 Respostas
- 2009 Exibições
- Última mensagem por Man Utd

Ter Jul 29, 2014 19:20
Cálculo: Limites, Derivadas e Integrais
-
- Limite de duas variaveis
por Tixa11 » Seg Abr 01, 2013 13:13
- 1 Respostas
- 2193 Exibições
- Última mensagem por young_jedi

Qua Abr 03, 2013 11:09
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Duas variaveis
por fabriel » Sáb Jun 15, 2013 16:48
- 2 Respostas
- 2489 Exibições
- Última mensagem por temujin

Sáb Jun 15, 2013 19:10
Cálculo: Limites, Derivadas e Integrais
-
- Limite de Função de Duas Variáveis
por raimundoocjr » Qui Out 10, 2013 22:29
- 0 Respostas
- 1653 Exibições
- Última mensagem por raimundoocjr

Qui Out 10, 2013 22:29
Cálculo: Limites, Derivadas e Integrais
-
- [Limite - Duas Variáveis (Indeterminação)]
por raimundoocjr » Qui Out 17, 2013 21:55
- 1 Respostas
- 3641 Exibições
- Última mensagem por Man Utd

Ter Jun 17, 2014 13:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



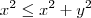 ,isto por sua vez implica
,isto por sua vez implica 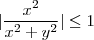 desde que
desde que  .Assim segue a função de duas variáveis definida pela expressão entre módulo é limitada por
.Assim segue a função de duas variáveis definida pela expressão entre módulo é limitada por  .Aplicando propriedades de limite obterá o resultado desejado.
.Aplicando propriedades de limite obterá o resultado desejado.
,isto por sua vez implica
desde que
.Assim segue a função de duas variáveis definida pela expressão entre módulo é limitada por
.Aplicando propriedades de limite obterá o resultado desejado.
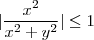 se a função tem denominador
se a função tem denominador 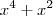

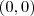 pela reta
pela reta  e pela parábola
e pela parábola  . Passando ao limite com
. Passando ao limite com  obterá dois resultados resultados distintos .
obterá dois resultados resultados distintos .
