Boa noite pessoal, estava resolvendo uma prova da UENP e achei este exercício, porem nao consigo desenvolve-lo para entao resolve-lo. Gostaria que me ajudassem a desenvolve-lo pois nao tenho nem kdeia por onde começar. Desde ja agradeço. Eis o exercício : 08. Um grupo de funcionários de uma empresa foi a um restaurante e gastou R$ 954,00. Na hora de pagar a conta, por uma questão de cavalheirismo, os homens dividiram igualmente o valor da conta e por isso cada um pagou R$ 5,85 a mais. Sabendo que o grupo tinha 13 mulheres, qual era o número de pessoas desse grupo?
a) 53
b) 40
c) 56
d) 50
e) 45




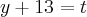
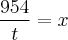


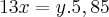

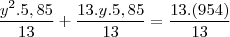
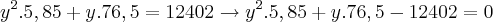





![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)