Eu sei as operações básicas:adição,subtração,divisão,potenciação,radiciação e etc.O problema é que eu não consigo aplicar isso nas expressões algébricas!
Por exemplo,em:
Eu não sei resolver porque não sei como isolar o t...Ele está elevado a um número e está negativo,deveria passa-lo para o outro lado como? Multiplicando? Dividindo? Sem fazer nada?
E o pior é que eu não acho nenhum material que explique isso,deve ser um negócio muito básico mesmo,estou me sentindo um retardado!
Outro exemplo de expressão é:
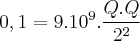
Eu não sei resolver esse tipo de coisa,na resolução o cara fez:
Eu entendi quando ele tirou a raiz,mas não entendi porque o 4 que era denominador do Q² virou numerador do 9!
Enfim,meu problema na maior parte são essas expressões elevadas a algo e que envolvem soma,adição,potência e etc,não sei qual operação prevalece.
Se puderem me ajudar,mesmo me mandando um link com esse tipo de expressão resolvida vocês estarão contribuindo muito,sério mesmo!
Obrigado!
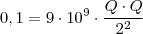
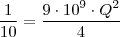
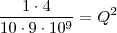
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.