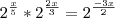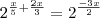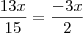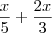por Adriana Baldussi » Seg Nov 23, 2009 14:41
por Adriana Baldussi » Seg Nov 23, 2009 14:41
![\[\sqrt[5]{2^{x}}.\sqrt[3]{4^{x}}=\sqrt8^{-x}
\sqrt[5]{2^{x}}.\sqrt[3]{(2^{2})^x}=\sqrt(2^3){-x}
\sqrt[5]{2^{x}}.\sqrt[3]{(2^{2})^x}=\sqrt2^-^3^x
2\tfrac{x}{5}.2\tfrac{2x}{3}=2\tfrac{-3x}{2} \[\sqrt[5]{2^{x}}.\sqrt[3]{4^{x}}=\sqrt8^{-x}
\sqrt[5]{2^{x}}.\sqrt[3]{(2^{2})^x}=\sqrt(2^3){-x}
\sqrt[5]{2^{x}}.\sqrt[3]{(2^{2})^x}=\sqrt2^-^3^x
2\tfrac{x}{5}.2\tfrac{2x}{3}=2\tfrac{-3x}{2}](/latexrender/pictures/97854dee4802f35174ef347b383dca4e.png)
E agora?
-
Adriana Baldussi
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Set 29, 2009 15:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Nov 23, 2009 15:29
por Molina » Seg Nov 23, 2009 15:29
Boa tarde, Adriana.
Só continuando da onde você parou:
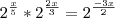
Da propriedade de exponencial...
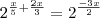

"Cortando" os 2's de ambos os lados...
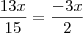
Chegamos que...


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Adriana Baldussi » Seg Nov 23, 2009 17:03
por Adriana Baldussi » Seg Nov 23, 2009 17:03
Só não entendi de onde surgiu o 13.
-
Adriana Baldussi
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Set 29, 2009 15:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Nov 23, 2009 17:07
por Molina » Seg Nov 23, 2009 17:07
Adriana Baldussi escreveu:Só não entendi de onde surgiu o 13.
Do mmc de
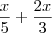
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1620 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2819 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2237 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
-
- Equação exponencial
por nan_henrique » Sáb Jul 10, 2010 13:00
- 1 Respostas
- 2184 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 13:12
Logaritmos
-
- Equação exponencial
por Moreno1986 » Sex Ago 06, 2010 14:48
- 1 Respostas
- 1447 Exibições
- Última mensagem por Moreno1986

Ter Ago 10, 2010 18:02
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\[\sqrt[5]{2^{x}}.\sqrt[3]{4^{x}}=\sqrt8^{-x}
\sqrt[5]{2^{x}}.\sqrt[3]{(2^{2})^x}=\sqrt(2^3){-x}
\sqrt[5]{2^{x}}.\sqrt[3]{(2^{2})^x}=\sqrt2^-^3^x
2\tfrac{x}{5}.2\tfrac{2x}{3}=2\tfrac{-3x}{2} \[\sqrt[5]{2^{x}}.\sqrt[3]{4^{x}}=\sqrt8^{-x}
\sqrt[5]{2^{x}}.\sqrt[3]{(2^{2})^x}=\sqrt(2^3){-x}
\sqrt[5]{2^{x}}.\sqrt[3]{(2^{2})^x}=\sqrt2^-^3^x
2\tfrac{x}{5}.2\tfrac{2x}{3}=2\tfrac{-3x}{2}](/latexrender/pictures/97854dee4802f35174ef347b383dca4e.png)

![\[\sqrt[5]{2^{x}}.\sqrt[3]{4^{x}}=\sqrt8^{-x}
\sqrt[5]{2^{x}}.\sqrt[3]{(2^{2})^x}=\sqrt(2^3){-x}
\sqrt[5]{2^{x}}.\sqrt[3]{(2^{2})^x}=\sqrt2^-^3^x
2\tfrac{x}{5}.2\tfrac{2x}{3}=2\tfrac{-3x}{2} \[\sqrt[5]{2^{x}}.\sqrt[3]{4^{x}}=\sqrt8^{-x}
\sqrt[5]{2^{x}}.\sqrt[3]{(2^{2})^x}=\sqrt(2^3){-x}
\sqrt[5]{2^{x}}.\sqrt[3]{(2^{2})^x}=\sqrt2^-^3^x
2\tfrac{x}{5}.2\tfrac{2x}{3}=2\tfrac{-3x}{2}](/latexrender/pictures/97854dee4802f35174ef347b383dca4e.png)