DETERMINE UMA FUNÇÃO
 , DEFINIDA NUM INTERVALO ABERTO
, DEFINIDA NUM INTERVALO ABERTO  , COM
, COM  , tal que
, tal que 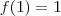 E, PARA TODO
E, PARA TODO  em
em  ,
, 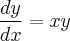 .
.Resolvi da seguinte maneira:
Primeiro, precisamos observar que
 . Por outro lado, temos que
. Por outro lado, temos que  . Notemos que
. Notemos que 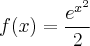 é uma possibilidade para satisfazer a proposta, contudo não satisfaz a condição de
é uma possibilidade para satisfazer a proposta, contudo não satisfaz a condição de 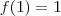 . Assim, façamos:
. Assim, façamos: 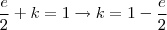 . Daí, temos:
. Daí, temos: 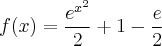 .
.Tem algo errado? O resultado não é este. Tentei fazer algumas manipulações algébricas, para tentar obter o mesmo resultado, mas não consegui nada.
A resposta certa é:
![y = \frac{1}{\sqrt[]{e}} {e}^{\frac{{x}^{2}}{2}} y = \frac{1}{\sqrt[]{e}} {e}^{\frac{{x}^{2}}{2}}](/latexrender/pictures/73aa0904f736844495365358b40127d4.png) .
.Obrigada.


 é uma função que satisfaz a propriedade dada , então
é uma função que satisfaz a propriedade dada , então 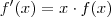 . Assumindo
. Assumindo 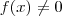 para quaisquer que seja
para quaisquer que seja  .Agora tente integrar ambos membros com relação a variável
.Agora tente integrar ambos membros com relação a variável ![[ln(f(x)) ]' = ln'(f(x)) \cdot f'(x) = f'(x)/f(x) [ln(f(x)) ]' = ln'(f(x)) \cdot f'(x) = f'(x)/f(x)](/latexrender/pictures/47a05ec721da8937bc59de6527408da9.png) (Regra da cadeia) , caso tenha dificuldade ver este resultado , faça uma substituição simples
(Regra da cadeia) , caso tenha dificuldade ver este resultado , faça uma substituição simples 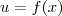 que resolve o problema .
que resolve o problema . conforme você notou , se tomarmos
conforme você notou , se tomarmos  (p/ alguma constante c real ) . Temos que
(p/ alguma constante c real ) . Temos que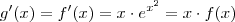 e
e 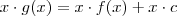
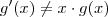 ,a igualdade ocorre somente quando
,a igualdade ocorre somente quando  já que estamos impondo que igualdade seja verdadeira para pontos arbitrários tomados no intervalo aberto
já que estamos impondo que igualdade seja verdadeira para pontos arbitrários tomados no intervalo aberto 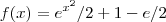 não satisfaz
não satisfaz 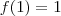 .
. não é verdadeira quando
não é verdadeira quando  , pois ,
, pois ,  . Entretanto,
. Entretanto, satisfaz
satisfaz 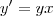 .
.


 .
.



