 por IlgssonBraga » Ter Nov 05, 2013 14:34
por IlgssonBraga » Ter Nov 05, 2013 14:34
Olá pessoal, alguém pode me ajudar nesse problema ?
Obtenha as equações da reta que passa pelo ponto A=(1,0,1) e intercepta a reta t : x=y=z+1 formando um ângulo de 60º.
Muito obrigado !
-
IlgssonBraga
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Jul 18, 2013 10:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por e8group » Sex Nov 15, 2013 12:25
por e8group » Sex Nov 15, 2013 12:25
Pensei da seguinte forma (Não tenho certeza se está correta ) . Seja

a reta a ser determinada que satisfaz as propriedades dadas no enunciado (Aqui estamos considerando B ponto de interseção entre às retas

e

[dada] ) .Vamos determinar o ponto

.Para isto , escolhemos um ponto

em

equidistante de

e

.Verifica-se sem dificuldade que o triângulo

é equilátero [/tex] , disto segue
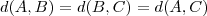
.
Se
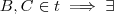
escalares

(distintos) tais que
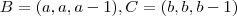
.
Temos
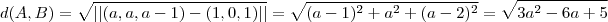
.
Analogamente ,
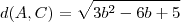
e

.
Assim ,

.
Logo ,


. Resolvendo esta equação determinará um possivél valor para

. Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria analítica estudo da reta distancia do ponta à reta
por jeffersonricardo » Dom Ago 22, 2010 08:29
- 1 Respostas
- 2415 Exibições
- Última mensagem por Pedro123

Seg Ago 23, 2010 22:24
Geometria Analítica
-
- [reta] geometria analítica
 por Leidiana Catum » Seg Jul 14, 2008 00:06
por Leidiana Catum » Seg Jul 14, 2008 00:06
- 1 Respostas
- 11919 Exibições
- Última mensagem por admin

Seg Jul 14, 2008 02:34
Geometria Analítica
-
- geometria analítica estudo da reta
por jeffersonricardo » Dom Ago 22, 2010 08:22
- 0 Respostas
- 1295 Exibições
- Última mensagem por jeffersonricardo

Dom Ago 22, 2010 08:22
Geometria Analítica
-
- [Geometria Analítica] Encontrar a reta t
por -civil- » Ter Ago 09, 2011 21:49
- 1 Respostas
- 2210 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 23:31
Geometria Analítica
-
- [Geometria Analitica] Equação de reta
por LucasSG » Qui Jun 06, 2013 22:45
- 1 Respostas
- 2212 Exibições
- Última mensagem por e8group

Sáb Jun 08, 2013 22:15
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 a reta a ser determinada que satisfaz as propriedades dadas no enunciado (Aqui estamos considerando B ponto de interseção entre às retas
a reta a ser determinada que satisfaz as propriedades dadas no enunciado (Aqui estamos considerando B ponto de interseção entre às retas  e
e  [dada] ) .Vamos determinar o ponto
[dada] ) .Vamos determinar o ponto  .Para isto , escolhemos um ponto
.Para isto , escolhemos um ponto  em
em  equidistante de
equidistante de  e
e  .Verifica-se sem dificuldade que o triângulo
.Verifica-se sem dificuldade que o triângulo  é equilátero [/tex] , disto segue
é equilátero [/tex] , disto segue 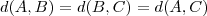 .
. 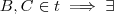 escalares
escalares  (distintos) tais que
(distintos) tais que 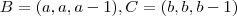 .
. 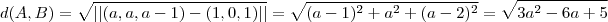 .
. 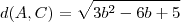 e
e  .
.  .
. 
 . Resolvendo esta equação determinará um possivél valor para
. Resolvendo esta equação determinará um possivél valor para  . Tente concluir .
. Tente concluir .
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.