![\int\frac{dx}{\sqrt[]{4x^2-49}} \int\frac{dx}{\sqrt[]{4x^2-49}}](/latexrender/pictures/1f9875a9e61005037a2fe8488411f41c.png) e tudo estava dando certo. Usei
e tudo estava dando certo. Usei  e
e 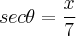 (para servir de referência para o final da resolução). Derivei o
(para servir de referência para o final da resolução). Derivei o  e substitui o dx. Aí ficou assim:
e substitui o dx. Aí ficou assim: ![\int\frac{7sec\theta tg\theta d\theta}{\sqrt[]{196sec^2\theta-49}} \int\frac{7sec\theta tg\theta d\theta}{\sqrt[]{196sec^2\theta-49}}](/latexrender/pictures/4f47eb7517597fb8197fb55b235ba4e7.png)
![\int\frac{7sec\theta tg\theta d\theta}{\sqrt[]{49(4sec^2\theta-1)}} \int\frac{7sec\theta tg\theta d\theta}{\sqrt[]{49(4sec^2\theta-1)}}](/latexrender/pictures/e11a29cae8993074cfbd2c09a5c0da1e.png)
![\int\frac{7sec\theta tg\theta d\theta}{\sqrt[]{49}*\sqrt[]{4sec^2\theta-1}} \int\frac{7sec\theta tg\theta d\theta}{\sqrt[]{49}*\sqrt[]{4sec^2\theta-1}}](/latexrender/pictures/0f0f810ba683aaf5a2369f88ba63f5c0.png)
![\int\frac{sec\theta tg\theta d\theta}{\sqrt[]{4sec^2\theta-1}} \int\frac{sec\theta tg\theta d\theta}{\sqrt[]{4sec^2\theta-1}}](/latexrender/pictures/24da9fbfa98825d2370b131d634fca1a.png) = OBS: eu tinha cancelado o 7 como termo unitário por causa da raíz quadrada de 49
= OBS: eu tinha cancelado o 7 como termo unitário por causa da raíz quadrada de 49A partir daqui virou outro problema: eu preciso agora de uma outra substituição e chamei o
 e derivei ela para subistituir o
e derivei ela para subistituir o 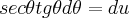 e assim ficou:
e assim ficou:![\int\frac{du}{\sqrt[]{4u^2-1}} \int\frac{du}{\sqrt[]{4u^2-1}}](/latexrender/pictures/21215219f3fede5e9e21942fa558da2d.png) e fatorei o
e fatorei o 
![\int\frac{du}{\sqrt[]{(2u-1)(2u+1)}} \int\frac{du}{\sqrt[]{(2u-1)(2u+1)}}](/latexrender/pictures/defaf216981e526e421322de3576177e.png) =
=![\int\frac{du}{\sqrt[]{2u-1}\sqrt[]{2u+1}} \int\frac{du}{\sqrt[]{2u-1}\sqrt[]{2u+1}}](/latexrender/pictures/94dca3edf4618ea3a9b9d38a105cef4e.png) =
=![\int\frac{du}{\sqrt[]{2u-1}} *\frac{1}{\sqrt[]{2u+1}} \int\frac{du}{\sqrt[]{2u-1}} *\frac{1}{\sqrt[]{2u+1}}](/latexrender/pictures/897aac462c950b050329dd31221653ea.png) =
=E parei aqui. Não tem como mais integrar pela substituição simples e muito menos por partes por causa da raíz do denominador na integral antes de eu fazer por substituição simples. Alguém poderia sugerir qual a substituição mais adequada depois da trigonométrica? Por muito pouco eu não consegui integrar

Bom, espero que vocês tenham compreendido o meu raciocínio e se puderem me ajudar, eu agradeço
Obrigado.


 o que implica
o que implica  . Agora note
. Agora note 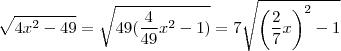 . Faça uma comparação deste resultado com a outra relação .Qual substituição deve tomar de modo escrever
. Faça uma comparação deste resultado com a outra relação .Qual substituição deve tomar de modo escrever  como
como 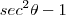 ?
?

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.