 por sasuyanli » Sáb Out 26, 2013 12:14
por sasuyanli » Sáb Out 26, 2013 12:14
Uma haste presa na origem do plano xy, ocupa a posição da reta x=ty. A haste intercepta a reta y=4 no ponto S e a elipse 4x²+(y-2)²=4 no ponto Q. Quando t varia, o vértice P do triângulo retângulo QPS descreve uma curva.
a) Escreva equações paramétricas dessa curva, em função do parâmetro t.
Não consegui chegar no resultado do gabarito dessa questão.
Fiz o seguinte:
Se y=4 e x=yt, então x(t)=4t.
E se a equação da elipse é definida por:
![[tex]4x^2+(y-2)^2=4\Rightarrow x^2+\frac{(y-2)^2}{4}=1\Rightarrow y^2t^2+\frac{y^2-4y+4}{4}=1\Rightarrow 4y^2t^2 + y^2- 4y +4 = 4 \Rightarrow 4y^2t^2 + y^2- 4y=0\Rightarrow y =\frac{x}{t} \Rightarrow \frac{x^2}{t^2} + 4x^2 - 4\frac{x}{t}=0 \Rightarrow x\left(\frac{x}{t^2} + 4x - \frac{4}{t} \right)=0 \Rightarrow \frac{x}{t^2} + 4x - \frac{4}{t}=0 \Rightarrow x\left(4+\frac{1}{t^2} \right)=\frac{4}{t} \Rightarrow x= \frac{4}{t}\ \times \frac{1}{\left 4t^2+1 \right} \Rightarrow y =\frac{4}{1+4t^2} [tex]4x^2+(y-2)^2=4\Rightarrow x^2+\frac{(y-2)^2}{4}=1\Rightarrow y^2t^2+\frac{y^2-4y+4}{4}=1\Rightarrow 4y^2t^2 + y^2- 4y +4 = 4 \Rightarrow 4y^2t^2 + y^2- 4y=0\Rightarrow y =\frac{x}{t} \Rightarrow \frac{x^2}{t^2} + 4x^2 - 4\frac{x}{t}=0 \Rightarrow x\left(\frac{x}{t^2} + 4x - \frac{4}{t} \right)=0 \Rightarrow \frac{x}{t^2} + 4x - \frac{4}{t}=0 \Rightarrow x\left(4+\frac{1}{t^2} \right)=\frac{4}{t} \Rightarrow x= \frac{4}{t}\ \times \frac{1}{\left 4t^2+1 \right} \Rightarrow y =\frac{4}{1+4t^2}](/latexrender/pictures/0adb4051dcf9476c38bc2f185a07c3db.png)
Porém, no gabarito a equação paramétrica da curva é
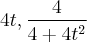
Gostaria de uma ajuda para saber onde errei.
Obrigada.
-
sasuyanli
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Jul 29, 2013 14:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: FÍSICA
- Andamento: cursando
 por e8group » Dom Nov 03, 2013 14:31
por e8group » Dom Nov 03, 2013 14:31
Também estou com a mesma dúvida ,resolvi este exercício da seguinte forma :
Supondo que a curva

(obtida pelo deslocamento do vértice P) tenha uma parametrização dada por
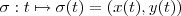
. Como o ponto

pertence simultaneamente a elipse e a reta
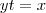
dada .Então , fazendo as contas conforme você fez , vamos obter
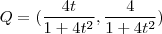
. Ora , os pontos
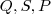
estão variando em conjunto de modo a preservar a ortogonalidade entre
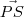
e

(estou utilizando este argumento para utilizar o próximo resultado afirmando que as ordenadas entre P,Q são iguais ) à medida que

varia . Logo ,
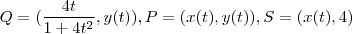
com
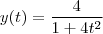
.
E facilmente obtemos
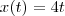
pelo que o ponto

pertence as duas retas dadas .
Vou conversar com meu prof. de cal. sobre este exercício .Obtendo resultados postarei .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [CURVAS] CÁLC II - Trajetórias e Parametrização
por inkz » Ter Nov 20, 2012 01:12
- 6 Respostas
- 4334 Exibições
- Última mensagem por inkz

Ter Nov 20, 2012 11:53
Cálculo: Limites, Derivadas e Integrais
-
- [CURVAS] Parametrização de elipse e vetores tangentes
por inkz » Ter Nov 20, 2012 04:43
- 2 Respostas
- 2758 Exibições
- Última mensagem por inkz

Qua Nov 21, 2012 03:25
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo - Parametrização
por Feliperpr » Ter Abr 24, 2012 21:14
- 12 Respostas
- 7489 Exibições
- Última mensagem por Feliperpr

Ter Abr 24, 2012 22:18
Cálculo: Limites, Derivadas e Integrais
-
- Parametrização de superfície
por AllanGeoffroy » Ter Mar 05, 2013 11:56
- 0 Respostas
- 894 Exibições
- Última mensagem por AllanGeoffroy

Ter Mar 05, 2013 11:56
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Vetorial - Parametrização] - Reta
por anselmojr97 » Dom Mar 20, 2016 01:25
- 0 Respostas
- 2513 Exibições
- Última mensagem por anselmojr97

Dom Mar 20, 2016 01:25
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![[tex]4x^2+(y-2)^2=4\Rightarrow x^2+\frac{(y-2)^2}{4}=1\Rightarrow y^2t^2+\frac{y^2-4y+4}{4}=1\Rightarrow 4y^2t^2 + y^2- 4y +4 = 4 \Rightarrow 4y^2t^2 + y^2- 4y=0\Rightarrow y =\frac{x}{t} \Rightarrow \frac{x^2}{t^2} + 4x^2 - 4\frac{x}{t}=0 \Rightarrow x\left(\frac{x}{t^2} + 4x - \frac{4}{t} \right)=0 \Rightarrow \frac{x}{t^2} + 4x - \frac{4}{t}=0 \Rightarrow x\left(4+\frac{1}{t^2} \right)=\frac{4}{t} \Rightarrow x= \frac{4}{t}\ \times \frac{1}{\left 4t^2+1 \right} \Rightarrow y =\frac{4}{1+4t^2} [tex]4x^2+(y-2)^2=4\Rightarrow x^2+\frac{(y-2)^2}{4}=1\Rightarrow y^2t^2+\frac{y^2-4y+4}{4}=1\Rightarrow 4y^2t^2 + y^2- 4y +4 = 4 \Rightarrow 4y^2t^2 + y^2- 4y=0\Rightarrow y =\frac{x}{t} \Rightarrow \frac{x^2}{t^2} + 4x^2 - 4\frac{x}{t}=0 \Rightarrow x\left(\frac{x}{t^2} + 4x - \frac{4}{t} \right)=0 \Rightarrow \frac{x}{t^2} + 4x - \frac{4}{t}=0 \Rightarrow x\left(4+\frac{1}{t^2} \right)=\frac{4}{t} \Rightarrow x= \frac{4}{t}\ \times \frac{1}{\left 4t^2+1 \right} \Rightarrow y =\frac{4}{1+4t^2}](/latexrender/pictures/0adb4051dcf9476c38bc2f185a07c3db.png)
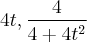


 (obtida pelo deslocamento do vértice P) tenha uma parametrização dada por
(obtida pelo deslocamento do vértice P) tenha uma parametrização dada por 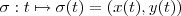 . Como o ponto
. Como o ponto  pertence simultaneamente a elipse e a reta
pertence simultaneamente a elipse e a reta 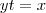 dada .Então , fazendo as contas conforme você fez , vamos obter
dada .Então , fazendo as contas conforme você fez , vamos obter 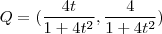 . Ora , os pontos
. Ora , os pontos 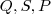 estão variando em conjunto de modo a preservar a ortogonalidade entre
estão variando em conjunto de modo a preservar a ortogonalidade entre 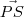 e
e  (estou utilizando este argumento para utilizar o próximo resultado afirmando que as ordenadas entre P,Q são iguais ) à medida que
(estou utilizando este argumento para utilizar o próximo resultado afirmando que as ordenadas entre P,Q são iguais ) à medida que  varia . Logo ,
varia . Logo , 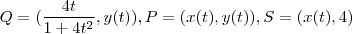 com
com 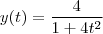 .
. 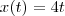 pelo que o ponto
pelo que o ponto  pertence as duas retas dadas .
pertence as duas retas dadas .