Olá....
Bom, para encontrarmos o valor do determinante de uma matriz, precisamos aplicar algumas propriedades, regras. Neste caso, temos duas matrizes quadradas, ou seja, apresentam duas linhas e duas colunas cada uma. Assim, para calcular os seus determinantes, basta aplicarmos uma regra bastante simples e ao mesmo tempo "difícil" de ser demonstrada, o que não vem ao caso. Tal regra consiste em, no caso de ser uma matriz quadrada de ORDEM 2, subtrair os resultados das multiplicações entre os números da diagonal principal e entre os da diagonal secundária. Para ficar mais claro:
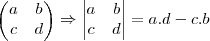
Agora, vamos ao caso do exercício em questão.
![\begin{pmatrix}
x & 4 \\
-3 & x+7
\end{pmatrix} \Rightarrow
\begin{vmatrix}
x & 4 \\
-3 & x+7
\end{vmatrix} = x(x+7)-[(-3).4]={x}^{2}+7x+12>0 \begin{pmatrix}
x & 4 \\
-3 & x+7
\end{pmatrix} \Rightarrow
\begin{vmatrix}
x & 4 \\
-3 & x+7
\end{vmatrix} = x(x+7)-[(-3).4]={x}^{2}+7x+12>0](/latexrender/pictures/43f0dd6940563a4d8d43b73c6be07f67.png)
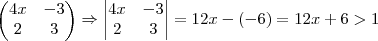
Assim, para concluir, precisamos resolver as duas inequações e o valor de x será o seguinte:
1°


Basta encontrarmos as raízes da equação
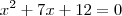
, observar o comportamento da sua curva, parábola que, neste caso, será voltada para cima, pois o coeficiente que acompanha

é positivo. Depois, precisamos analisar qual é o intervalo tal que os valores de x possuem imagem y positiva e quando possuem imagem y negativa. Então, obteremos o intervalo que satisfaz a inequação em questão.
Resolvendo a equação, aplicando a Fórmula de Bhaskara, temos:



Então, as raízes da equação são -3 e -4. Contudo, seria melhor se conseguisse mostrar o comportamento da parábola através de um gráfico (tente fazer ou use GeoGebra ou qualquer outro programa que construa gráficos e ,então, ficará mais visível). Logo, o intervalo que satisfaz a inequação em questão é:
![]-\infty;-4[ ]-\infty;-4[](/latexrender/pictures/f6966d235d85c6b554c544cf4e33062a.png)
e
![]-3;+\infty[ ]-3;+\infty[](/latexrender/pictures/11258254bbb33a79df87a7e09e877dcd.png)
2°
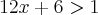
Observemos que, como não é do segundo grau, torna-se mais simples de resolver, bastando apenas:

Note que
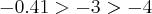
.
Então, o intervalo que satisfaz a inequação em questão é:
![]-\frac{5}{12};+\infty[ ]-\frac{5}{12};+\infty[](/latexrender/pictures/8d5996802b2a1c10a94ba6b88ee05d6b.png)
Agora que já temos os intervalos nos quais os valores de x satisfazem as inequações, então:
(Como queremos detA>0 E detB>1....)
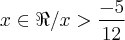 .
.Este é o resultado.... Se quiser perguntar sobre alguma passagem que talvez não tenha entendido ou quiser mostrar algum erro.... Espero ter ajudado.

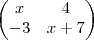
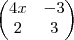

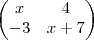
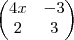

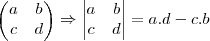
![\begin{pmatrix}
x & 4 \\
-3 & x+7
\end{pmatrix} \Rightarrow
\begin{vmatrix}
x & 4 \\
-3 & x+7
\end{vmatrix} = x(x+7)-[(-3).4]={x}^{2}+7x+12>0 \begin{pmatrix}
x & 4 \\
-3 & x+7
\end{pmatrix} \Rightarrow
\begin{vmatrix}
x & 4 \\
-3 & x+7
\end{vmatrix} = x(x+7)-[(-3).4]={x}^{2}+7x+12>0](/latexrender/pictures/43f0dd6940563a4d8d43b73c6be07f67.png)
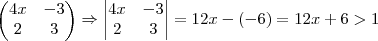

 Basta encontrarmos as raízes da equação
Basta encontrarmos as raízes da equação 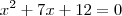 , observar o comportamento da sua curva, parábola que, neste caso, será voltada para cima, pois o coeficiente que acompanha
, observar o comportamento da sua curva, parábola que, neste caso, será voltada para cima, pois o coeficiente que acompanha  é positivo. Depois, precisamos analisar qual é o intervalo tal que os valores de x possuem imagem y positiva e quando possuem imagem y negativa. Então, obteremos o intervalo que satisfaz a inequação em questão.
é positivo. Depois, precisamos analisar qual é o intervalo tal que os valores de x possuem imagem y positiva e quando possuem imagem y negativa. Então, obteremos o intervalo que satisfaz a inequação em questão.


![]-\infty;-4[ ]-\infty;-4[](/latexrender/pictures/f6966d235d85c6b554c544cf4e33062a.png) e
e ![]-3;+\infty[ ]-3;+\infty[](/latexrender/pictures/11258254bbb33a79df87a7e09e877dcd.png)
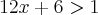

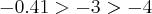 .
.![]-\frac{5}{12};+\infty[ ]-\frac{5}{12};+\infty[](/latexrender/pictures/8d5996802b2a1c10a94ba6b88ee05d6b.png)
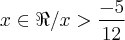 .
.



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.