 por zaspers » Ter Out 08, 2013 07:02
por zaspers » Ter Out 08, 2013 07:02
Desculpem-me por questionar algo tão simples, mas tenho dificuldade em compreender estas questões.
Preciso resolver a seguinte equação:

- Na tentativa de igualar as bases fatorei o

ficando assim:
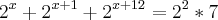
Contudo, não sei como resolver a parte exponencial do lado esquerdo da igualdade. Alguém poderia me dar um norte?
Ciente da atenção de todos, desde já agradeço.
-
zaspers
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Out 08, 2013 06:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por Russman » Qua Out 09, 2013 04:17
por Russman » Qua Out 09, 2013 04:17
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por zaspers » Sáb Out 12, 2013 10:26
por zaspers » Sáb Out 12, 2013 10:26
Sim digitei. Desculpa a demora para responder, época de provas! rs
Eu acabei conseguindo fazer, mas creio que minha nota na prova não foi das melhores. Log acabou comigo.
De qualquer forma, muito obrigado!
-
zaspers
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Out 08, 2013 06:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Exponencial - Dúvida na resolução!
por jamiel » Dom Mai 15, 2011 14:09
- 1 Respostas
- 4775 Exibições
- Última mensagem por Claudin

Dom Mai 15, 2011 14:21
Funções
-
- [porcentagem] Auxilio na solução do problema
por rafynhasantos » Sáb Jun 21, 2008 22:58
- 1 Respostas
- 1585 Exibições
- Última mensagem por Molina

Sáb Jun 21, 2008 23:29
Álgebra Elementar
-
- Venha em meu auxílio Oh grande mestre!
 por zenildo » Qui Mai 12, 2016 23:04
por zenildo » Qui Mai 12, 2016 23:04
- 3 Respostas
- 3176 Exibições
- Última mensagem por Cleyson007

Qua Mai 18, 2016 16:08
Trigonometria
-
- Auxílio - Derivada de equação implícita
por Charles Vigne » Qui Jul 25, 2019 16:13
- 0 Respostas
- 3026 Exibições
- Última mensagem por Charles Vigne

Qui Jul 25, 2019 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] derivada de exponencial
por beel » Sáb Out 15, 2011 22:20
- 4 Respostas
- 2794 Exibições
- Última mensagem por beel

Qua Out 19, 2011 11:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 ficando assim:
ficando assim: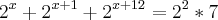


 , onde
, onde  é um número Real.
é um número Real.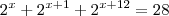
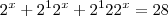
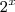 é fator comum de todas as parcelas você pode fatorá-lo de forma que
é fator comum de todas as parcelas você pode fatorá-lo de forma que
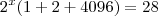


 e sim um
e sim um  a solução seria mais elegante. Veja que se a equação fosse
a solução seria mais elegante. Veja que se a equação fosse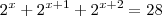
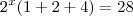
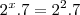
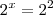


 .
. ,
,  e para
e para  ,
,  .
.
 , monte a função e substitua
, monte a função e substitua  por
por  .
.
