 por Nuno_Martins » Sáb Nov 21, 2009 18:27
por Nuno_Martins » Sáb Nov 21, 2009 18:27
Estou com uma dúvida que até deve ser bastante fácil de resolver, mas não consigo compreender.
Como posso calcular os termos de uma Matriz?
Tenho aqui que por exemplo tomando esta matriz:
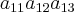
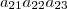

Os termos da matriz são:

Podem-me ajudar e dizerem-me como consigo chegar a este resultado?
-
Nuno_Martins
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Nov 21, 2009 18:08
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por Molina » Dom Nov 22, 2009 12:11
por Molina » Dom Nov 22, 2009 12:11
Amigo, não entendi muito bem esta questão.
Poderia colocá-la inteira?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Nuno_Martins » Dom Nov 22, 2009 12:27
por Nuno_Martins » Dom Nov 22, 2009 12:27
Na matéria teórica que a professora nos deu têm uma matriz genérica, igual a essa que ai coloquei e depois tem os termos dessa matriz, iguais aos que eu ai coloquei também.
A minha dúvida é como é que eu posso chegar aos termos da matriz. Não compreendo qual é a "fórmula" para lá poder chegar.
-
Nuno_Martins
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Nov 21, 2009 18:08
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por Molina » Dom Nov 22, 2009 13:20
por Molina » Dom Nov 22, 2009 13:20
Isso aí tá parecendo mais o algorítmo para calcular o determinante de uma matriz de ordem 3x3.
Sinceramente, da forma que você escreveu eu nunca vi antes. Espero que alguém possa te ajudar.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Li_P » Qua Dez 09, 2009 17:40
por Li_P » Qua Dez 09, 2009 17:40
Olá Nuno_Martins,
Bom, eu acho que isso foi feito dessa maneira:
foi feita a multiplicação na diagonal.
na frente da matriz vc repete a primeira e a segunda coluna
depois é só multiplicar na diagonal da esquerda para a direita e depois da direita para a esquerda
assim:
a11 a22 a33; a12 a23 a31; a13 a21 a33 (esses são os elementos da multiplicação dos termos da esquerda para a direita)
a12 a21 a33; a11 a23 a32; a13 a22 a31 (esses são os elementos da multiplicação dos termos da direita para a esquerda)
tem outros jeitos para se chegar a isso, mas esse é o que eu sempre usei.
Espero ter ajudado.
Liii
..."Por estranho que possa parecer, o poder das Matemáticas reside no fato de que elas se obtém de todo o pensamento inútil e economizam admiravelmente as operações mentais."...
-

Li_P
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Nov 19, 2009 16:54
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Ciência da Computação
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- termo
por uspsilva » Sex Mar 13, 2009 13:10
- 1 Respostas
- 6054 Exibições
- Última mensagem por Neperiano

Sex Set 17, 2010 15:44
Pedidos de Materiais
-
- termo I
por uspsilva » Qua Mar 18, 2009 15:17
- 1 Respostas
- 2784 Exibições
- Última mensagem por Neperiano

Ter Out 25, 2011 17:39
Pedidos de Materiais
-
- termo e algebra I
por uspsilva » Ter Abr 14, 2009 11:28
- 1 Respostas
- 2643 Exibições
- Última mensagem por Neperiano

Sáb Set 17, 2011 12:14
Pedidos de Materiais
-
- TERMO INDEPENDENTE DE X
por hudeslan » Seg Ago 17, 2009 19:28
- 2 Respostas
- 22078 Exibições
- Última mensagem por Molina

Seg Ago 17, 2009 23:18
Estatística
-
- Primeiro Termo da P.G.
por Cleyson007 » Seg Out 12, 2009 17:14
- 1 Respostas
- 2074 Exibições
- Última mensagem por Molina

Seg Out 12, 2009 23:30
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
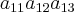
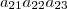



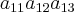
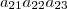











 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.