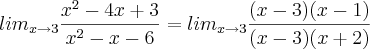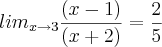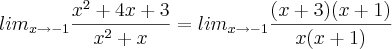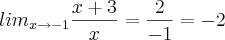por Claudia Sotero » Sáb Nov 21, 2009 22:09
por Claudia Sotero » Sáb Nov 21, 2009 22:09
Olá pessoal, eu tenho muita dificuldade nestes exercícios de limite com fatoração, e gostaria de ajuda, já tentei de todas as formas, mas na hora de fatorar o bicho pega.
Desde já agradeço a todos[/color]
x² - 4x = 3 / x² - x - 6 (lim. x= 3)
x / x² - 2x (lim x = 0)
x² + 4x + 3 / x² + x (lim x = -1)
-
Claudia Sotero
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Nov 20, 2009 16:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por jonathan carvalho » Dom Nov 22, 2009 12:10
por jonathan carvalho » Dom Nov 22, 2009 12:10
Olá pessoal, eu tenho muita dificuldade nestes exercícios de limite com fatoração, e gostaria de ajuda, já tentei de todas as formas, mas na hora de fatorar o bicho pega.
Desde já agradeço a todos
x² - 4x = 3 / x² - x - 6 (lim. x= 3)
x / x² - 2x (lim x = 0)
x² + 4x + 3 / x² + x (lim x = -1)[/quote]
-
jonathan carvalho
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Nov 22, 2009 11:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por jonathan carvalho » Dom Nov 22, 2009 12:27
por jonathan carvalho » Dom Nov 22, 2009 12:27
Por favor,,se tiver alguem on line me ajudem com alguns calculos.....obrigado...
GC5,2= 5!/2!x 3!=5.4.3!/2.3!(corta o 4 com o 2 e o 3! Com o 3!)=10
C7,3= 7!/3! . 4!=7.6.5.4!/3.2 x 4!(corta o 6 com o 3.2 e o 4! Com o 4!)=35
35.10=350
o x e o . significa vezes
-
jonathan carvalho
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Nov 22, 2009 11:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- AJUDA NESTE EXERCÍCIO, POR FAVOR!
 por LVPM » Ter Nov 22, 2016 18:11
por LVPM » Ter Nov 22, 2016 18:11
- 2 Respostas
- 2297 Exibições
- Última mensagem por Cleyson007

Qua Nov 23, 2016 11:41
Funções
-
- me ajudem neste exercício de limite
por Claudia Sotero » Sex Nov 20, 2009 16:15
- 2 Respostas
- 4219 Exibições
- Última mensagem por Claudia Sotero

Sáb Nov 21, 2009 10:47
Computação
-
- Alguem pode me ajudar neste exercício, por favor...
por caducustodio » Sex Ago 17, 2012 09:00
- 1 Respostas
- 1808 Exibições
- Última mensagem por Cleyson007

Sex Ago 17, 2012 09:50
Sistemas de Equações
-
- [trigonometria] exercicio, me ajudem por favor?
por amanda s » Sex Nov 15, 2013 20:15
- 1 Respostas
- 7203 Exibições
- Última mensagem por nakagumahissao

Sáb Nov 16, 2013 00:50
Trigonometria
-
- [calculo] ajudem urgente por favor nesse exercicio
por amanda s » Sáb Nov 16, 2013 17:27
- 1 Respostas
- 1995 Exibições
- Última mensagem por nakagumahissao

Dom Nov 17, 2013 10:04
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.