Sejam A, B, e Mn (R) e a £ R, mostre que:
a)(A^t)^t = A
b)(
A)^t = A^t, onde ? K c)Se n=m, (A.B)^t = B^T . A^T
por Knoner » Dom Set 29, 2013 19:49
A)^t = A^t, onde ? K 
por e8group » Seg Set 30, 2013 21:52
![[A]_{ij} = a_{ij}](/latexrender/pictures/696f564a2df9d77962db1d56d1f617c8.png "[A]_{ij} = a_{ij}")
para designar o termo geral da matriz e lembrando da definição de transposição de matrizes : ![[A^t]_{ij} = [A]_{ji} = a_{ji}](/latexrender/pictures/bb4429fd8d2c473fce86883ea5eeeef3.png "[A^t]_{ij} = [A]_{ji} = a_{ji}")
(**) , temos que ![[(A^t)^t]_{ij} = [A^t]_{ji} = [A]_{ij} = a_{ij}](/latexrender/pictures/a968c7178a1e4963ea162d4561724979.png "[(A^t)^t]_{ij} = [A^t]_{ji} = [A]_{ij} = a_{ij}")
para todo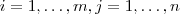 
o que mostra 
. No item b , utilize a definição (**) + propriedades dos números reais ,se não conseguir post . No item c , basta intercambiar a definição (**) juntamente com a definição produto de matrizes . Veja minha sugestão , ![[(AB)^t]_{ij} = [AB]_{ji} = \sum_{k=1}^n a_{jk} \cdot b_{ki}](/latexrender/pictures/164a9a91760a9c2213b4421a97d2384f.png "[(AB)^t]_{ij} = [AB]_{ji} = \sum_{k=1}^n a_{jk} \cdot b_{ki}")
. Sendo o produto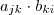 
comutativo (pois ,
são números reais) e utilizando resultado do item (a) , ![a_{jk} = [A^t]_{kj} , b_{kj} = [B^t]_{jk}](/latexrender/pictures/bcc05bba66e675b80521c5cf67d26370.png "a_{jk} = [A^t]_{kj} , b_{kj} = [B^t]_{jk}")
. Seguindo estas dicas conseguirá concluir o exercício .
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)