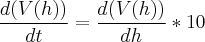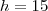por Ana Maria da Silva » Sáb Set 28, 2013 14:22
por Ana Maria da Silva » Sáb Set 28, 2013 14:22
A areia que vaza de um depósito forma uma pilha cônica cuja altura é sempre igual ao dobro do raio da sua base. Se a altura da pilha aumenta a uma taxa de 10cm/min, então qual é a taxa com que a areia está escoando quando a altura da pilha for 15cm? Obs: Dê o resultado, a menos do \pi, até a primeira casa decimal.
Preciso ver o desenvolvimento!
-
Ana Maria da Silva
- Usuário Parceiro

-
- Mensagens: 83
- Registrado em: Qua Mar 27, 2013 15:09
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Russman » Sáb Set 28, 2013 16:33
por Russman » Sáb Set 28, 2013 16:33
Calcule o volume da pilha em função da sua altura. Derive e encontre a relação entre a taxa de escoamento e a da variação da altura.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Ana Maria da Silva » Sáb Set 28, 2013 17:21
por Ana Maria da Silva » Sáb Set 28, 2013 17:21
Não consegui desenvolver! se possível queria ver o desenvolvimento.Agradeço...
-
Ana Maria da Silva
- Usuário Parceiro

-
- Mensagens: 83
- Registrado em: Qua Mar 27, 2013 15:09
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Man Utd » Sáb Set 28, 2013 20:13
por Man Utd » Sáb Set 28, 2013 20:13
Ana Maria da Silva escreveu:A areia que vaza de um depósito forma uma pilha cônica cuja altura é sempre igual ao dobro do raio da sua base. Se a altura da pilha aumenta a uma taxa de 10cm/min, então qual é a taxa com que a areia está escoando quando a altura da pilha for 15cm? Obs: Dê o resultado, a menos do \pi, até a primeira casa decimal.
Preciso ver o desenvolvimento!
o volume de um cone é dado por:
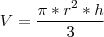
, o enunciado disse que
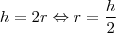
, então

agora bastar fazer:
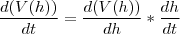
repare que

ficando com:
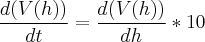
tente terminar lembrando que
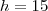
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Helicóptero e uma cônica
por kesinhazzz » Seg Dez 14, 2009 16:21
- 1 Respostas
- 1483 Exibições
- Última mensagem por Elcioschin

Ter Dez 15, 2009 13:31
Geometria Analítica
-
- identificação de uma cônica
por Danilo » Qua Jan 16, 2013 10:16
- 1 Respostas
- 1822 Exibições
- Última mensagem por young_jedi

Qua Jan 16, 2013 16:21
Geometria Analítica
-
- Barraca cônica
por Luiz 2017 » Sex Set 22, 2017 20:40
- 0 Respostas
- 1147 Exibições
- Última mensagem por Luiz 2017

Sex Set 22, 2017 20:40
Cálculo: Limites, Derivadas e Integrais
-
- [hipérbole / cônica] Funções
 por Cleyson007 » Sáb Set 06, 2008 01:32
por Cleyson007 » Sáb Set 06, 2008 01:32
- 1 Respostas
- 2654 Exibições
- Última mensagem por admin

Ter Set 09, 2008 15:35
Funções
-
- [conica] achar a equação da parábola
 por Ge_dutra » Sáb Mar 16, 2013 21:47
por Ge_dutra » Sáb Mar 16, 2013 21:47
- 4 Respostas
- 3268 Exibições
- Última mensagem por Ge_dutra

Qua Abr 03, 2013 00:06
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



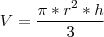 , o enunciado disse que
, o enunciado disse que 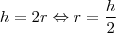 , então
, então 
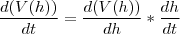
 ficando com:
ficando com: