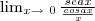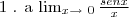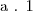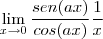por Nicolas1Lane » Qui Set 26, 2013 07:56
por Nicolas1Lane » Qui Set 26, 2013 07:56
Dada a seguinte proposição

queria saber se minha resolução apresentada abaixo matematicamente descrita é aceitável ou ainda se poderia ser melhorada ou mesmo no caso da existência, me digam dicas para melhorar ainda mais neste aprendizado...
Estou sendo meio redundante, mas isso se deve a enfatização de minha professora de querer que todas as propriedades e etapas de resoluções usadas nos cálculos sejam explicitadas até que se chegue ao produto final.
Assim:

=
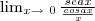
=

=
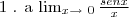
=
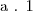
=

-
Nicolas1Lane
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Set 11, 2013 23:25
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: Exatas/Ciência da Computação
- Andamento: cursando
 por young_jedi » Qui Set 26, 2013 14:08
por young_jedi » Qui Set 26, 2013 14:08
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite - usando apenas limites notáveis
por emsbp » Seg Jul 23, 2012 16:45
- 2 Respostas
- 1975 Exibições
- Última mensagem por emsbp

Ter Jul 24, 2012 16:50
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limites notáveis -->compreender a propriedade usada
por Nicolas1Lane » Qua Set 25, 2013 20:11
- 2 Respostas
- 1799 Exibições
- Última mensagem por Nicolas1Lane

Qua Set 25, 2013 20:45
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] Resolução de questão
por malumayara » Qua Set 12, 2012 15:10
- 3 Respostas
- 1921 Exibições
- Última mensagem por MarceloFantini

Qua Set 12, 2012 19:15
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Exercício com limites notáveis
por fff » Sáb Fev 08, 2014 21:41
- 3 Respostas
- 2672 Exibições
- Última mensagem por e8group

Dom Fev 09, 2014 15:29
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Calcular 2 limites notáveis
por fff » Sex Abr 11, 2014 14:26
- 4 Respostas
- 2517 Exibições
- Última mensagem por fff

Sex Abr 11, 2014 19:12
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 queria saber se minha resolução apresentada abaixo matematicamente descrita é aceitável ou ainda se poderia ser melhorada ou mesmo no caso da existência, me digam dicas para melhorar ainda mais neste aprendizado...
queria saber se minha resolução apresentada abaixo matematicamente descrita é aceitável ou ainda se poderia ser melhorada ou mesmo no caso da existência, me digam dicas para melhorar ainda mais neste aprendizado...