 por lucianofloripa » Sex Nov 20, 2009 12:38
por lucianofloripa » Sex Nov 20, 2009 12:38
Determine o(s) valor(es) que "r" deve assumir para que o ponto (r,2) diste cinco unidades do ponto (0,-2).
-
lucianofloripa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Nov 20, 2009 12:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Arquitetura UFSC
- Andamento: formado
 por Cleyson007 » Sex Nov 20, 2009 13:04
por Cleyson007 » Sex Nov 20, 2009 13:04
Boa tarde Luciano!
A fórmula da distância entre dois pontos é:
![d(a,b)=\sqrt[2]{{({x}_{2}-{x}_{1})}^{2}+({y}_{2}-{y}_{1})^2} d(a,b)=\sqrt[2]{{({x}_{2}-{x}_{1})}^{2}+({y}_{2}-{y}_{1})^2}](/latexrender/pictures/9b48877ce3b6fd72cfbb4ced2edf289e.png)
Jogando na fórmula, temos:
![5=\sqrt[2]{{(0-r)}^{2}+{(-2-2)}^{2}} 5=\sqrt[2]{{(0-r)}^{2}+{(-2-2)}^{2}}](/latexrender/pictures/855ee6b0da9f16c3fccc111c91f9a329.png)
![5=\sqrt[2]{{r}^{2}+16} 5=\sqrt[2]{{r}^{2}+16}](/latexrender/pictures/3188cff322e280311d98337bb6f8ece0.png)
Para tirar as raiz, eleve ambos os lados ao quadrado:
![{5}^{2}=(\sqrt[2]{{r}^{2}+16})^2 {5}^{2}=(\sqrt[2]{{r}^{2}+16})^2](/latexrender/pictures/afb627d6646a3da344994451bcea3295.png)
A partir daí, tente resolver

Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por lucianofloripa » Sex Nov 20, 2009 14:51
por lucianofloripa » Sex Nov 20, 2009 14:51
sim o resultado é esse mesmo + ou - 3
mas só pra eu entender...o r² não da pra cortar pela raiz ?
só mais uma duvida, fora desse conteudo, pois acho que estou pecando no sinal...
0 - 1 = m ( 0 - 4 )
- 1 = - 4m
-1/4 = m
o resultado é -1/4 ou 1/4 ?
-
lucianofloripa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Nov 20, 2009 12:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Arquitetura UFSC
- Andamento: formado
 por Cleyson007 » Sex Nov 20, 2009 18:36
por Cleyson007 » Sex Nov 20, 2009 18:36
Boa tarde Luciano!
Meu caro Luciano, você
não pode "cortar" o r² devido serem dois termos dentro da raiz.
Quanto a segunda dúvida -->
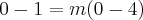

Aí que está sua dúvida -->
Lembra que o m não pode ficar negativo?Para o m não ficar negativo, devemos multiplicar a expressão por (-1).. quando uma expressão é multiplicada por (-1), invertem-se todos os sinais. Daí, o resultado correto é:
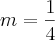
.
Comente qualquer dúvida

Não deixe de participar do Fórum, ok?
Ótimo final de semana

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por lucianofloripa » Qua Nov 25, 2009 11:30
por lucianofloripa » Qua Nov 25, 2009 11:30
Cleyson mais uma questão que não consigo resolver !!
Qual é a equação da reta que passa pelo ponto P (6,-4) e é paralela à bissetriz dos quadrantes pares ?
-
lucianofloripa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Nov 20, 2009 12:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Arquitetura UFSC
- Andamento: formado
 por lucianofloripa » Qua Nov 25, 2009 14:33
por lucianofloripa » Qua Nov 25, 2009 14:33
mais uma duvida !!!
Determine a equação da reta perpendicular à reta de equação 2x + 3y - 6 = 0 no ponto em que esta intercepta o eixo das abscissas.
resolvendo...
y = -2x/3 + 6/3 => logo coeficiente angular da equação que intercepta é -2/3
m1 = - 1/m2
-2/3 = -1/m2 => logo coeficiente angular da equação perpendicular é 3/2
suponho que o valor de x da equação perpendicular seja zero, pois intercepta o eixo das ordenada !!
minha dificuldade é saber o valor de y, para aplicar na formula !!
-
lucianofloripa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Nov 20, 2009 12:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Arquitetura UFSC
- Andamento: formado
 por lucianofloripa » Qui Nov 26, 2009 11:25
por lucianofloripa » Qui Nov 26, 2009 11:25
JA CONSEGUI RESOLVER TUDO !! FALTOU UM POUCO DE INTERPRETAÇÃO MESMO !! RSRS.. VALEU !
-
lucianofloripa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Nov 20, 2009 12:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Arquitetura UFSC
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determine m e n
por Cleyson007 » Qua Mai 20, 2009 13:28
- 4 Respostas
- 5183 Exibições
- Última mensagem por Cleyson007

Sex Mai 29, 2009 10:03
Números Complexos
-
- Determine k
por Cleyson007 » Qui Jun 11, 2009 12:57
- 2 Respostas
- 2317 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 13:19
Polinômios
-
- Determine MN
por Balanar » Seg Ago 30, 2010 01:36
- 0 Respostas
- 1184 Exibições
- Última mensagem por Balanar

Seg Ago 30, 2010 01:36
Álgebra Elementar
-
- determine a lei
por brunoscollaro » Sáb Out 22, 2011 11:58
- 1 Respostas
- 1359 Exibições
- Última mensagem por MarceloFantini

Sáb Out 22, 2011 15:16
Funções
-
- Determine a e b
por jcmatematica » Seg Ago 04, 2014 22:52
- 1 Respostas
- 3490 Exibições
- Última mensagem por Russman

Ter Ago 05, 2014 17:30
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![d(a,b)=\sqrt[2]{{({x}_{2}-{x}_{1})}^{2}+({y}_{2}-{y}_{1})^2} d(a,b)=\sqrt[2]{{({x}_{2}-{x}_{1})}^{2}+({y}_{2}-{y}_{1})^2}](/latexrender/pictures/9b48877ce3b6fd72cfbb4ced2edf289e.png)
![5=\sqrt[2]{{(0-r)}^{2}+{(-2-2)}^{2}} 5=\sqrt[2]{{(0-r)}^{2}+{(-2-2)}^{2}}](/latexrender/pictures/855ee6b0da9f16c3fccc111c91f9a329.png)
![5=\sqrt[2]{{r}^{2}+16} 5=\sqrt[2]{{r}^{2}+16}](/latexrender/pictures/3188cff322e280311d98337bb6f8ece0.png)
![{5}^{2}=(\sqrt[2]{{r}^{2}+16})^2 {5}^{2}=(\sqrt[2]{{r}^{2}+16})^2](/latexrender/pictures/afb627d6646a3da344994451bcea3295.png)




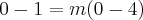

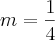 .
.




