 por felipemreis » Sex Set 13, 2013 13:29
por felipemreis » Sex Set 13, 2013 13:29
Estou com dúvida na seguinte questão:

Mostre que f é função de 1 grau:
a)f(x)= (x-6)^2-(x-3)*(x-6)
b)f(x)= 2x^3+2x/3x^2+3
EU TENTEI RESOLVER OS POLINÔMIOS DE CADA FUNÇÃO, MAS EU NÃO CONSEGUI CHEGAR A UMA RESPOSTA COERENTE!
NÃO SEI COMO RESOLVER, POR FAVOR ME AJUDEM!

- Essa é a imagem da questão que eu escanei do livro, mostra a questão.
-
felipemreis
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Set 13, 2013 13:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por temujin » Sex Set 13, 2013 15:22
por temujin » Sex Set 13, 2013 15:22
Olá.
Procure colocar sempre uma questão por tópico. Aumenta as chances de que alguém responda sua dúvida. Vamos lá:
a)
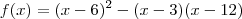
Desenvolva os polinômios:
![f(x) = [x^2-12x+36]-[x^2-15x+72] = 3x-36 f(x) = [x^2-12x+36]-[x^2-15x+72] = 3x-36](/latexrender/pictures/e73d57121e5f0f5ed63dd26893f7577d.png)
Onde a segunda parte é obtida apenas aplicando a distributiva.
b)
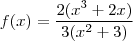
Aqui vc pode começar pensando em fatorar os polinômios. Veja que tanto no numerador quanto no denominador vc tem alguma coisa em comum entre os termos. No numerador 2x aparece em cada um dos termos e no caso do denominador 3 aparece em cada um dos termos, então comece por aí.
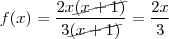
-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
 por Russman » Sex Set 13, 2013 17:40
por Russman » Sex Set 13, 2013 17:40
Na letra b) suponha que
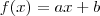
. Assim,
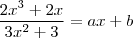
donde
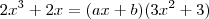
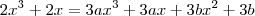
Daí, por igualdade de polinômios, temos
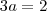
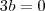
Logo,
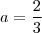
e

. De fato, a função é de 1° grau e
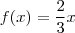
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por felipemreis » Sex Set 13, 2013 19:56
por felipemreis » Sex Set 13, 2013 19:56
Obrigado! temujin. Esclareceu as minhas dúvidas. Mas segundo o livro a resposta correta da letra a é: f(x)=3x. Foi diferente da sua resposta!
-
felipemreis
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Set 13, 2013 13:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por temujin » Sex Set 13, 2013 19:59
por temujin » Sex Set 13, 2013 19:59
felipemreis escreveu:Obrigado! temujin. Esclareceu as minhas dúvidas. Mas segundo o livro a resposta correta da letra a é: f(x)=3x. Foi diferente da sua resposta!
Claro, engano meu. Veja que o produto do segundo termo é 3.12 = 36

-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
 por felipemreis » Sáb Set 14, 2013 01:13
por felipemreis » Sáb Set 14, 2013 01:13
-
felipemreis
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Set 13, 2013 13:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função] isso é função do segundo grau?
por maulakalanata » Qua Mar 27, 2013 04:03
- 1 Respostas
- 2280 Exibições
- Última mensagem por timoteo

Qua Mar 27, 2013 10:51
Funções
-
- [Função 1°grau] determinar função.
por Thiago 86 » Ter Abr 23, 2013 11:27
- 2 Respostas
- 2406 Exibições
- Última mensagem por Thiago 86

Ter Abr 23, 2013 13:05
Funções
-
- Função do 2° Grau
por mimi2009 » Qua Jun 10, 2009 05:46
- 1 Respostas
- 2086 Exibições
- Última mensagem por Molina

Qua Jun 10, 2009 08:05
Funções
-
- Função do 2 grau...
por Fiel8 » Qua Jul 01, 2009 21:34
- 4 Respostas
- 3440 Exibições
- Última mensagem por Cleyson007

Qui Jul 02, 2009 16:16
Funções
-
- Função 1° grau
por DanielFerreira » Ter Set 22, 2009 14:14
- 2 Respostas
- 2137 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 19:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


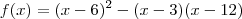
![f(x) = [x^2-12x+36]-[x^2-15x+72] = 3x-36 f(x) = [x^2-12x+36]-[x^2-15x+72] = 3x-36](/latexrender/pictures/e73d57121e5f0f5ed63dd26893f7577d.png)
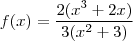
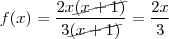

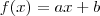 . Assim,
. Assim,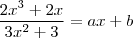
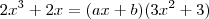
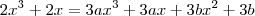
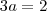
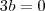
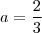 e
e  . De fato, a função é de 1° grau e
. De fato, a função é de 1° grau e 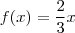 .
.




![(x-6)^2 = [x^2-12x+36] (x-6)^2 = [x^2-12x+36]](/latexrender/pictures/c259c876cbbaa9ddf2cd238b5fd1c7c1.png)
![(x-3)(x-12)=[x^2-15x+36] (x-3)(x-12)=[x^2-15x+36]](/latexrender/pictures/a81e963d2a6bb1115f49de764052eff1.png)
![f(x) = [x^2-12x+36]-[x^2-15x+36] = 3x f(x) = [x^2-12x+36]-[x^2-15x+36] = 3x](/latexrender/pictures/1611066d30e3283b36437ce479dc36f6.png)







 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.