a)f(x)= (x-6)^2-(x-3)*(x-6)
b)f(x)= 2x^3+2x/3x^2+3
EU TENTEI RESOLVER OS POLINÔMIOS DE CADA FUNÇÃO, MAS EU NÃO CONSEGUI CHEGAR A UMA RESPOSTA COERENTE!
NÃO SEI COMO RESOLVER, POR FAVOR ME AJUDEM!


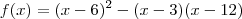
![f(x) = [x^2-12x+36]-[x^2-15x+72] = 3x-36 f(x) = [x^2-12x+36]-[x^2-15x+72] = 3x-36](/latexrender/pictures/e73d57121e5f0f5ed63dd26893f7577d.png)
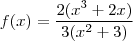
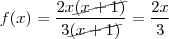

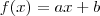 . Assim,
. Assim,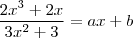
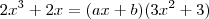
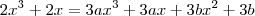
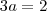
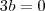
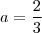 e
e  . De fato, a função é de 1° grau e
. De fato, a função é de 1° grau e 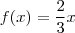 .
.

felipemreis escreveu:Obrigado! temujin. Esclareceu as minhas dúvidas. Mas segundo o livro a resposta correta da letra a é: f(x)=3x. Foi diferente da sua resposta!



![(x-6)^2 = [x^2-12x+36] (x-6)^2 = [x^2-12x+36]](/latexrender/pictures/c259c876cbbaa9ddf2cd238b5fd1c7c1.png)
![(x-3)(x-12)=[x^2-15x+36] (x-3)(x-12)=[x^2-15x+36]](/latexrender/pictures/a81e963d2a6bb1115f49de764052eff1.png)
![f(x) = [x^2-12x+36]-[x^2-15x+36] = 3x f(x) = [x^2-12x+36]-[x^2-15x+36] = 3x](/latexrender/pictures/1611066d30e3283b36437ce479dc36f6.png)





Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)