 por lucasbyno » Sex Set 13, 2013 01:49
por lucasbyno » Sex Set 13, 2013 01:49
Não sei escrever fórmula no latex então vai assim mesmo:
limite quando x tende a 0 de
raíz quádrupla de (x^4 + 1) -(menos)
raiz quadrada de (x^2 +1) e tudo isso dividido por
x^2.
Eu nunca consigo resolver limites quando há raiz, alguém poderia me dar uma dica, um macete (além da resolução desse exemplo acima)? Também seria bom se me dissessem um macete ou uma "forma correta de raciocinar" quando há limites com raiz quadrada ou cúbica no denominador. São as minhas maiores dificuldades.

-
lucasbyno
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Set 11, 2013 00:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por Man Utd » Dom Set 15, 2013 00:41
por Man Utd » Dom Set 15, 2013 00:41
lucasbyno escreveu:Não sei escrever fórmula no latex então vai assim mesmo:
limite quando x tende a 0 de
raíz quádrupla de (x^4 + 1) -(menos)
raiz quadrada de (x^2 +1) e tudo isso dividido por
x^2.
Eu nunca consigo resolver limites quando há raiz, alguém poderia me dar uma dica, um macete (além da resolução desse exemplo acima)? Também seria bom se me dissessem um macete ou uma "forma correta de raciocinar" quando há limites com raiz quadrada ou cúbica no denominador. São as minhas maiores dificuldades.

olá. Por favor utilize nas futuras postagens o Latex para facilitar na compreensão.
![\\\\\\ \lim_{x\rightarrow0} \frac{\sqrt[4]{x^{4}+1}-\sqrt{x^{2}+1}}{x^{2}} \\\\\\ \lim_{x\rightarrow0} \frac{(\sqrt[4]{x^{4}+1}-\sqrt{x^{2}+1})*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})} \\\\\\ \lim_{x\rightarrow0} \frac{\sqrt{x^{4}+1}-(x^{2}+1)}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})} \\\\\\ \lim_{x\rightarrow0} \frac{(\sqrt{x^{4}+1}-(x^{2}+1))*(\sqrt{x^{4}+1}+(x^{2}+1))}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})*(\sqrt{x^{4}+1}+(x^{2}+1))} \\\\\\ \lim_{x\rightarrow0} \frac{x^{4}+1-(x^{2}+1)^{2}}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})*(\sqrt{x^{4}+1}+(x^{2}+1))} \\\\\\ \lim_{x\rightarrow0} \frac{\sqrt[4]{x^{4}+1}-\sqrt{x^{2}+1}}{x^{2}} \\\\\\ \lim_{x\rightarrow0} \frac{(\sqrt[4]{x^{4}+1}-\sqrt{x^{2}+1})*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})} \\\\\\ \lim_{x\rightarrow0} \frac{\sqrt{x^{4}+1}-(x^{2}+1)}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})} \\\\\\ \lim_{x\rightarrow0} \frac{(\sqrt{x^{4}+1}-(x^{2}+1))*(\sqrt{x^{4}+1}+(x^{2}+1))}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})*(\sqrt{x^{4}+1}+(x^{2}+1))} \\\\\\ \lim_{x\rightarrow0} \frac{x^{4}+1-(x^{2}+1)^{2}}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})*(\sqrt{x^{4}+1}+(x^{2}+1))}](/latexrender/pictures/5ea96d5f10c2ba50b1e6a2e7d7998df1.png)
dá pra terminar?
Sobre a dica,algumas vezes uma substituição de variáveis resolve e outras tbm pode ser resolvido pela identidade
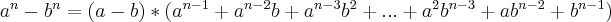
att

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por lucasbyno » Dom Set 15, 2013 14:15
por lucasbyno » Dom Set 15, 2013 14:15
Man Utd escreveu:Sobre a dica,algumas vezes uma substituição de variáveis resolve e outras tbm pode ser resolvido pela identidade
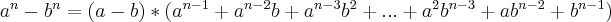
att

Ajudou muito!
Mas eu não entendi muito essa última parte... Substituição de variáveis? E o que tem o binômio de Newton a ver com isso?
-
lucasbyno
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Set 11, 2013 00:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por Man Utd » Dom Set 15, 2013 16:13
por Man Utd » Dom Set 15, 2013 16:13
lucasbyno escreveu:Man Utd escreveu:Sobre a dica,algumas vezes uma substituição de variáveis resolve e outras tbm pode ser resolvido pela identidade
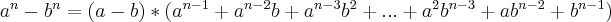
att

Ajudou muito!
Mas eu não entendi muito essa última parte... Substituição de variáveis? E o que tem o binômio de Newton a ver com isso?
Bem vc já viu limites de funções compostas correto? quando eu disse substituição de variáveis me referir a isso.Sobre esta identidade é muito útil,fica difícil de explicar aqui,o melhor seria se houvesse um exemplo,tenho certeza que ainda irá se deparar com alguns desse limites.
att.

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2786 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] - Dúvida sobre o resultado de um limite
por Paulo Souza » Dom Ago 25, 2013 20:57
- 0 Respostas
- 1839 Exibições
- Última mensagem por Paulo Souza

Dom Ago 25, 2013 20:57
Cálculo: Limites, Derivadas e Integrais
-
- Sobre Limites
por thiagosaadoficial » Seg Fev 29, 2016 17:08
- 0 Respostas
- 1546 Exibições
- Última mensagem por thiagosaadoficial

Seg Fev 29, 2016 17:08
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda sobre limites
 por MJC » Ter Mai 06, 2008 12:41
por MJC » Ter Mai 06, 2008 12:41
- 8 Respostas
- 18571 Exibições
- Última mensagem por admin

Qua Mai 07, 2008 00:58
Cálculo: Limites, Derivadas e Integrais
-
- Questão sobre limites
por Paulod22 » Seg Mar 07, 2011 01:18
- 6 Respostas
- 4289 Exibições
- Última mensagem por Paulod22

Ter Mar 08, 2011 10:55
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![\\\\\\ \lim_{x\rightarrow0} \frac{\sqrt[4]{x^{4}+1}-\sqrt{x^{2}+1}}{x^{2}} \\\\\\ \lim_{x\rightarrow0} \frac{(\sqrt[4]{x^{4}+1}-\sqrt{x^{2}+1})*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})} \\\\\\ \lim_{x\rightarrow0} \frac{\sqrt{x^{4}+1}-(x^{2}+1)}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})} \\\\\\ \lim_{x\rightarrow0} \frac{(\sqrt{x^{4}+1}-(x^{2}+1))*(\sqrt{x^{4}+1}+(x^{2}+1))}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})*(\sqrt{x^{4}+1}+(x^{2}+1))} \\\\\\ \lim_{x\rightarrow0} \frac{x^{4}+1-(x^{2}+1)^{2}}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})*(\sqrt{x^{4}+1}+(x^{2}+1))} \\\\\\ \lim_{x\rightarrow0} \frac{\sqrt[4]{x^{4}+1}-\sqrt{x^{2}+1}}{x^{2}} \\\\\\ \lim_{x\rightarrow0} \frac{(\sqrt[4]{x^{4}+1}-\sqrt{x^{2}+1})*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})} \\\\\\ \lim_{x\rightarrow0} \frac{\sqrt{x^{4}+1}-(x^{2}+1)}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})} \\\\\\ \lim_{x\rightarrow0} \frac{(\sqrt{x^{4}+1}-(x^{2}+1))*(\sqrt{x^{4}+1}+(x^{2}+1))}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})*(\sqrt{x^{4}+1}+(x^{2}+1))} \\\\\\ \lim_{x\rightarrow0} \frac{x^{4}+1-(x^{2}+1)^{2}}{x^{2}*(\sqrt[4]{x^{4}+1}+\sqrt{x^{2}+1})*(\sqrt{x^{4}+1}+(x^{2}+1))}](/latexrender/pictures/5ea96d5f10c2ba50b1e6a2e7d7998df1.png)
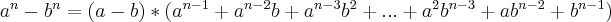

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
