Transformação em Produto + Sistema

[theriut]

Determine os números reais x e y, com e , tais que :
{ senx.seny = -1/4
{ cos(x+y) + cos(x-y)= -3/2

Eu consegui fazer mas o resultado não bate com o gabarito que é :
e
ou
E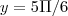

A minha resolução :

senx.seny = -1/4 =
-2senx.seny = 1/2 =
-(transformando em soma)>
{ cos(x+y) - cos(x-y) = 1/2 }
Aí fica o sistema :
cos(x+y) - cos(x-y ) = 1/2
cos (x+y ) + cos(x-y) = -3/2
Somando as duas equações fica 2cos(x+y) = -1
cos(x+y) = -1/2
Como x+y n deve ultrapassar pi, então x+y deveria ser 120graus (unico grau pequeno q tem cosseno -1/2 ).Como os valores de x e y do gabarito nao somam 120, parei de fazer a questão.

ALguma luz galera ?
Vlw

[Elcioschin]

senx*seny = - 1/4 ----> senx = - 1/4*seny ----> sen²x = 1/16*sen²y

cos²x = 1 - sen²x ----> cos²x = 1 - 1/16*sen²y ----> 16*cos²x = (16*sen²y - 1)/sen²y ----> Equação I

cos(x + y) + cos(x - y)= - 3/2 ----> (cosx*cosy - senx*seny) + (cosx*cosy + senx*seny) = - 3/2

2*cosx*cosy = - 3/2 -----> 4*cosx*cosy = - 3 ----> 16*cos²x*cos²y = 9 ----> Substituindo I:

[(16*sen²y - 1)/sen²y]*cos²y = 9 ----> (16*sen²y - 1)*(1 - sen²y) = 9*sen²y

16*(sen²y)² - 8*sen²y + 1 = 0 ----> Bhaskara ----> sen²x = 1/4 ----> seny = + 1/2 (1º e 2º quadrantes)

y = pi/6 ou y = 5*pi/6

senx*seny = - 1/4 ----> senx*(+1/2) = - 1/4 ----> senx = - 1/2 ----> x = - pi/6 ou x = - 5*pi/6

Bateu com o gabarito.

[theriut]

Muito obrigado amigo, tá aí um bom método pra resolução.Eu só queria entender aonde errei na minha resolução =/
No mais, mt obrigado.

[Elcioschin]

Vou mostrar o seu errro:

senx.seny = -1/4 =
-2senx.seny = 1/2 =
-(transformando em soma)>
{ cos(x+y) - cos(x-y) = 1/2 }

Este foi o erro: esta transformação NÃO existe

Uma transformação possível seria ----> cosp + cosq = 2*[cos(p+q)/2]*[cos(p-q)/2]

Neste caso bastaria fazer, na 2ª equação, p = x + y e q = x - y :

cos(x+y) + cos(x-y) = - 3/2 ----> 2*cos[(x+y) + (x-y)]*cos[(x+ y) - (x-y)] = 2*cos(2x)*cos(2y) = 2*(1-2sen²x)*(1 - 2*sen²y)

Agora basta substituir sen²x por sen²y (da 1ª equação) e resolver de modo similar ao meu modo anterior.

[theriut]

Po, quando eu desenvolvo a expressão :
cos(x+y) - cos(x-y)
fica :( cosx.cosy - senx.seny ) - (cosx.cosy + senx.seny)
q somando devidamente, fica -2senx.seny,ou seja, da pra garantir que cos(x+y) - cos(x-y) = -2senx.seny
Só não sei pq o método não está sendo eficaz na resolução do problema.
Abraços

[Elcioschin]

Agora você errou no sinal ----> trocou + por - na 2ª equação:

cos(x + y) + cos(x - y) = cosx*cosy - senx*seny + cosx*cosy - senx*seny = 2*cosx*cosy

[theriut]

Ué, mas o "-" da segunda equação entre ( cosx.cosy - senx.seny ) e (cosx.cosy + senx.seny) é pq estamos calculando [cos(x+y)] - [cos(x-y)].Não entendi pq teria q ser o sinal de mais entre ( cosx.cosy - senx.seny ) e (cosx.cosy + senx.seny). Me desculpe se não estou conseguindo enxergar um erro BEM simples q eu esteja cometendo mas ja tentei.
Abraços

[Elcioschin]

Meu caro

Veja a sua mensagem ORIGINAL:

Determine os números reais x e y, com 0 =< x + y =< pi e 0 =< y =< pi, tais que :
{ senx.seny = -1/4
{ cos(x+y) + cos(x-y)= -3/2

Note que o sinal na SEGUNDA equação é +

A partir daí você passou a escrever o sinal - o que resultou nos seus erros!!!!