 por theriut » Seg Nov 16, 2009 05:22
por theriut » Seg Nov 16, 2009 05:22
Determine os números reais x e y, com

e

, tais que :
{ senx.seny = -1/4
{ cos(x+y) + cos(x-y)= -3/2
Eu consegui fazer mas o resultado não bate com o gabarito que é :

e

ou

E
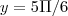
A minha resolução :
senx.seny = -1/4 =
-2senx.seny = 1/2 =
-(transformando em soma)>
{ cos(x+y) - cos(x-y) = 1/2 }
Aí fica o sistema :
cos(x+y) - cos(x-y ) = 1/2
cos (x+y ) + cos(x-y) = -3/2
Somando as duas equações fica 2cos(x+y) = -1
cos(x+y) = -1/2
Como x+y n deve ultrapassar pi, então x+y deveria ser 120graus (unico grau pequeno q tem cosseno -1/2 ).Como os valores de x e y do gabarito nao somam 120, parei de fazer a questão.
ALguma luz galera ?
Vlw
Editado pela última vez por
theriut em Ter Nov 17, 2009 03:36, em um total de 1 vez.
-
theriut
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Nov 16, 2009 05:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Seg Nov 16, 2009 18:13
por Elcioschin » Seg Nov 16, 2009 18:13
senx*seny = - 1/4 ----> senx = - 1/4*seny ----> sen²x = 1/16*sen²y
cos²x = 1 - sen²x ----> cos²x = 1 - 1/16*sen²y ----> 16*cos²x = (16*sen²y - 1)/sen²y ----> Equação I
cos(x + y) + cos(x - y)= - 3/2 ----> (cosx*cosy - senx*seny) + (cosx*cosy + senx*seny) = - 3/2
2*cosx*cosy = - 3/2 -----> 4*cosx*cosy = - 3 ----> 16*cos²x*cos²y = 9 ----> Substituindo I:
[(16*sen²y - 1)/sen²y]*cos²y = 9 ----> (16*sen²y - 1)*(1 - sen²y) = 9*sen²y
16*(sen²y)² - 8*sen²y + 1 = 0 ----> Bhaskara ----> sen²x = 1/4 ----> seny = + 1/2 (1º e 2º quadrantes)
y = pi/6 ou y = 5*pi/6
senx*seny = - 1/4 ----> senx*(+1/2) = - 1/4 ----> senx = - 1/2 ----> x = - pi/6 ou x = - 5*pi/6
Bateu com o gabarito.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por theriut » Ter Nov 17, 2009 03:37
por theriut » Ter Nov 17, 2009 03:37
Muito obrigado amigo, tá aí um bom método pra resolução.Eu só queria entender aonde errei na minha resolução =/
No mais, mt obrigado.
-
theriut
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Nov 16, 2009 05:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Ter Nov 17, 2009 08:53
por Elcioschin » Ter Nov 17, 2009 08:53
Vou mostrar o seu errro:
senx.seny = -1/4 =
-2senx.seny = 1/2 =
-(transformando em soma)>
{ cos(x+y) - cos(x-y) = 1/2 }
Este foi o erro: esta transformação NÃO existe
Uma transformação possível seria ----> cosp + cosq = 2*[cos(p+q)/2]*[cos(p-q)/2]
Neste caso bastaria fazer, na 2ª equação, p = x + y e q = x - y :
cos(x+y) + cos(x-y) = - 3/2 ----> 2*cos[(x+y) + (x-y)]*cos[(x+ y) - (x-y)] = 2*cos(2x)*cos(2y) = 2*(1-2sen²x)*(1 - 2*sen²y)
Agora basta substituir sen²x por sen²y (da 1ª equação) e resolver de modo similar ao meu modo anterior.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por theriut » Ter Nov 17, 2009 18:10
por theriut » Ter Nov 17, 2009 18:10
Po, quando eu desenvolvo a expressão :
cos(x+y) - cos(x-y)
fica :( cosx.cosy - senx.seny ) - (cosx.cosy + senx.seny)
q somando devidamente, fica -2senx.seny,ou seja, da pra garantir que cos(x+y) - cos(x-y) = -2senx.seny
Só não sei pq o método não está sendo eficaz na resolução do problema.
Abraços
-
theriut
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Nov 16, 2009 05:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Qua Nov 18, 2009 08:48
por Elcioschin » Qua Nov 18, 2009 08:48
Agora você errou no sinal ----> trocou + por - na 2ª equação:
cos(x + y) + cos(x - y) = cosx*cosy - senx*seny + cosx*cosy - senx*seny = 2*cosx*cosy
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por theriut » Qua Nov 18, 2009 21:10
por theriut » Qua Nov 18, 2009 21:10
Ué, mas o "-" da segunda equação entre ( cosx.cosy - senx.seny ) e (cosx.cosy + senx.seny) é pq estamos calculando [cos(x+y)] - [cos(x-y)].Não entendi pq teria q ser o sinal de mais entre ( cosx.cosy - senx.seny ) e (cosx.cosy + senx.seny). Me desculpe se não estou conseguindo enxergar um erro BEM simples q eu esteja cometendo mas ja tentei.
Abraços
-
theriut
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Nov 16, 2009 05:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Qui Nov 19, 2009 11:33
por Elcioschin » Qui Nov 19, 2009 11:33
Meu caro
Veja a sua mensagem ORIGINAL:
Determine os números reais x e y, com 0 =< x + y =< pi e 0 =< y =< pi, tais que :
{ senx.seny = -1/4
{ cos(x+y) + cos(x-y)= -3/2
Note que o sinal na SEGUNDA equação é +
A partir daí você passou a escrever o sinal - o que resultou nos seus erros!!!!
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Transformação em produto
 por Ananda » Seg Mar 24, 2008 17:31
por Ananda » Seg Mar 24, 2008 17:31
- 3 Respostas
- 5512 Exibições
- Última mensagem por Ananda

Ter Mar 25, 2008 14:55
Trigonometria
-
- Transformação em produto.
 por lucassouza » Qui Jul 02, 2015 21:00
por lucassouza » Qui Jul 02, 2015 21:00
- 1 Respostas
- 1918 Exibições
- Última mensagem por DanielFerreira

Sáb Jul 04, 2015 15:53
Trigonometria
-
- [Transformação Linear] Nucleo e Imagem, ache a transformaçao
por vualas » Qua Nov 07, 2012 00:37
- 2 Respostas
- 4248 Exibições
- Última mensagem por adauto martins

Qui Dez 15, 2016 11:12
Álgebra Linear
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4946 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3084 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  , tais que :
, tais que :  e
e 
 E
E 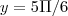





 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.