 por -Sarah- » Seg Ago 19, 2013 20:32
por -Sarah- » Seg Ago 19, 2013 20:32
Determine a área do triângulo ABC e a medida do lado a. É um triângulo acutângulo, de lados b e c valendo,
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
e
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
, respectivamente. E o ângulo A vale 75º.
-
-Sarah-
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Fev 23, 2013 18:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Seg Ago 19, 2013 22:41
por young_jedi » Seg Ago 19, 2013 22:41
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por -Sarah- » Ter Ago 20, 2013 21:05
por -Sarah- » Ter Ago 20, 2013 21:05
-
-Sarah-
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Fev 23, 2013 18:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Ter Ago 20, 2013 21:13
por young_jedi » Ter Ago 20, 2013 21:13
é isso ai mesmo
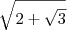
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por -Sarah- » Ter Ago 20, 2013 21:14
por -Sarah- » Ter Ago 20, 2013 21:14
Ah! Vlw
-
-Sarah-
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Fev 23, 2013 18:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por -Sarah- » Ter Ago 20, 2013 21:21
por -Sarah- » Ter Ago 20, 2013 21:21
E como eu calculo a área?
-
-Sarah-
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Fev 23, 2013 18:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Ter Ago 20, 2013 23:48
por young_jedi » Ter Ago 20, 2013 23:48
a área é dada por
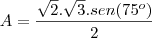
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resolução de triângulos quaisquer.
por rodsales » Dom Nov 15, 2009 18:45
- 1 Respostas
- 6809 Exibições
- Última mensagem por Lucio Carvalho

Seg Nov 16, 2009 10:56
Trigonometria
-
- (Fuvest) Relações Métricas em Triângulos Quaisquer - Ajudem!
 por kamillanjb » Sex Jul 22, 2011 15:00
por kamillanjb » Sex Jul 22, 2011 15:00
- 1 Respostas
- 6983 Exibições
- Última mensagem por FilipeCaceres

Sex Jul 22, 2011 21:18
Geometria Plana
-
- [Área de triângulos]
 por Gustavo Gomes » Seg Fev 03, 2014 22:37
por Gustavo Gomes » Seg Fev 03, 2014 22:37
- 1 Respostas
- 2135 Exibições
- Última mensagem por young_jedi

Ter Fev 04, 2014 15:30
Geometria Plana
-
- [Triângulos] Determinação de área
por Gustavo Gomes » Dom Mai 25, 2014 20:14
- 0 Respostas
- 1160 Exibições
- Última mensagem por Gustavo Gomes

Dom Mai 25, 2014 20:14
Trigonometria
-
- [Semelhança de triângulos] Triângulos quadrados
 por Debora Bruna » Seg Ago 08, 2016 12:18
por Debora Bruna » Seg Ago 08, 2016 12:18
- 0 Respostas
- 1473 Exibições
- Última mensagem por Debora Bruna

Seg Ago 08, 2016 12:18
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) e
e ![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) , respectivamente. E o ângulo A vale 75º.
, respectivamente. E o ângulo A vale 75º.
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) e
e ![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) , respectivamente. E o ângulo A vale 75º.
, respectivamente. E o ângulo A vale 75º.
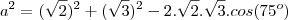
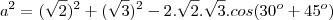
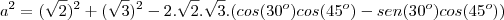
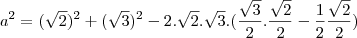

![{a}^{2}= 2+3 - 2 \sqrt[]{6}(\frac{\sqrt[]{6}}{4}-\frac{\sqrt[]{2}}{4}) {a}^{2}= 2+3 - 2 \sqrt[]{6}(\frac{\sqrt[]{6}}{4}-\frac{\sqrt[]{2}}{4})](/latexrender/pictures/b5a9b7161d41b1b4cad001a4800b2c2d.png)
![{a}^{2}= 5 - \frac{2\sqrt[]{6}.\sqrt[]{6}}{4}+ \frac{2\sqrt[]{6}.\sqrt[]{2}}{4} {a}^{2}= 5 - \frac{2\sqrt[]{6}.\sqrt[]{6}}{4}+ \frac{2\sqrt[]{6}.\sqrt[]{2}}{4}](/latexrender/pictures/d46c0794099e84d2fc228092e43c416e.png)
![{a}^{2}= 5 - \frac{12}{4}+ \frac{2.2\sqrt[]{3}}{4} {a}^{2}= 5 - \frac{12}{4}+ \frac{2.2\sqrt[]{3}}{4}](/latexrender/pictures/07348305be12f987c1d6e401b620e1ff.png)
![a = \sqrt[]{5 - 3 +\sqrt[]{3}} a = \sqrt[]{5 - 3 +\sqrt[]{3}}](/latexrender/pictures/60ea977ac3e83441e2afd943450b5982.png)

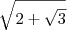



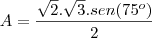


 .
.
 :
: