 por nakagumahissao » Qui Ago 15, 2013 11:04
por nakagumahissao » Qui Ago 15, 2013 11:04
Pessoal, não consegui resolver esta questão. Apenas consegui o esboço do gráfico que se trata de uma esfera e de um cone. O cone limita a parte inferior e parte da esfera, o limite superior.
Poderiam me ajudar por favor? A questão é a seguinte:
Calcule a integral:
![{I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV {I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV](/latexrender/pictures/db5b81b4fc0f561bab447ff493098c67.png)
Onde R é a região limitada por:
![z = \sqrt[]{2 - {x}^{2} - {y}^{2}} z = \sqrt[]{2 - {x}^{2} - {y}^{2}}](/latexrender/pictures/e1128b31491a40f553d7021da41db36f.png)
e
![z = \sqrt[]{{x}^{2} + {y}^{2}} z = \sqrt[]{{x}^{2} + {y}^{2}}](/latexrender/pictures/593fda6c93daf33d4379ead6624bbe20.png)
Tentei utilizar coordenadas esféricas, mas obtive uma coisa muito complicada de se resolver. Alguém saberia resolver esta questão?
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por young_jedi » Sex Ago 16, 2013 15:51
por young_jedi » Sex Ago 16, 2013 15:51
minha sugestão é uma mudança para coordenadas polares
ai teríamos que

e
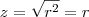
então a integral ficaria
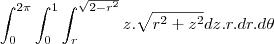
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por nakagumahissao » Sex Ago 16, 2013 16:35
por nakagumahissao » Sex Ago 16, 2013 16:35
Young_Jedi,
Vou tentar com polares, apesar de que o exercício foi dado para utilizarmos as coordenadas esféricas ou cilíndricas. Qualquer dúvida volto aqui novamente. Por enquanto, muitíssimo obrigado pela sua resposta.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por mecfael » Dom Ago 18, 2013 00:43
por mecfael » Dom Ago 18, 2013 00:43
Vamos usar coordenadas Cilíndricas para montar a integral, como temos uma região compreendida entre dois sólidos:
Onde o sólido de baixo

(cone)
E o sólido de cima é
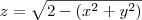
(esfera na origem de raio r²=2)
E a intersecção é igual a:

Uma circunferencia de raio r=1 no plano z=1, ou seja, as região será dividida da origem entre a parte do cone

até z=1, e de z=1 até
a esfera
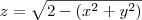
Então as regiões em coordenadas cilindricas

e
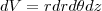
e

temos:

e
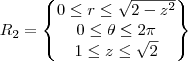
Os limites de R1 são os mesmos do cone, então é inútil explicar como achei, os limites de R2 temos que

então se isolar o r temos que
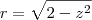
e verificamos que é verdade, pois em z=1, temos que o r=1 pois estamos na fronteira entre os dois sólidos que é a circunferência de raio r=1, e

temos que r=0, pois é o máximo da região R2, agora que achamos R1 e R2 vamos montar a integral I dividida entre duas regiões:
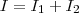
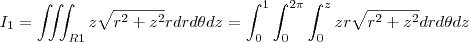
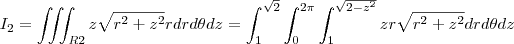
Essas integrais se resolvem com substituição simples fazendo
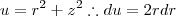
e de forma análoga para a variável z.
-
mecfael
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Ago 17, 2013 23:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integrais Triplas
por wyncler » Sex Jul 03, 2009 23:04
- 0 Respostas
- 8674 Exibições
- Última mensagem por wyncler

Sex Jul 03, 2009 23:04
Cálculo: Limites, Derivadas e Integrais
-
- Integrais triplas
por ah001334 » Dom Dez 04, 2011 17:43
- 4 Respostas
- 3653 Exibições
- Última mensagem por ah001334

Dom Dez 04, 2011 19:05
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAIS TRIPLAS]
por carvalhothg » Sex Mai 04, 2012 11:23
- 1 Respostas
- 2137 Exibições
- Última mensagem por MarceloFantini

Sáb Mai 05, 2012 00:29
Cálculo: Limites, Derivadas e Integrais
-
- Integrais Triplas
por gilijgs » Ter Nov 24, 2015 20:03
- 0 Respostas
- 2662 Exibições
- Última mensagem por gilijgs

Ter Nov 24, 2015 20:03
Cálculo: Limites, Derivadas e Integrais
-
- Mudança de variaveis em integrais duplas e triplas
por luiz3d » Qui Out 08, 2009 17:09
- 0 Respostas
- 3818 Exibições
- Última mensagem por luiz3d

Qui Out 08, 2009 17:09
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV {I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV](/latexrender/pictures/db5b81b4fc0f561bab447ff493098c67.png)
![z = \sqrt[]{2 - {x}^{2} - {y}^{2}} z = \sqrt[]{2 - {x}^{2} - {y}^{2}}](/latexrender/pictures/e1128b31491a40f553d7021da41db36f.png)
![z = \sqrt[]{{x}^{2} + {y}^{2}} z = \sqrt[]{{x}^{2} + {y}^{2}}](/latexrender/pictures/593fda6c93daf33d4379ead6624bbe20.png)

![{I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV {I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV](/latexrender/pictures/db5b81b4fc0f561bab447ff493098c67.png)
![z = \sqrt[]{2 - {x}^{2} - {y}^{2}} z = \sqrt[]{2 - {x}^{2} - {y}^{2}}](/latexrender/pictures/e1128b31491a40f553d7021da41db36f.png)
![z = \sqrt[]{{x}^{2} + {y}^{2}} z = \sqrt[]{{x}^{2} + {y}^{2}}](/latexrender/pictures/593fda6c93daf33d4379ead6624bbe20.png)


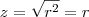
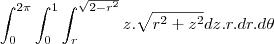


 (cone)
(cone)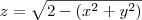 (esfera na origem de raio r²=2)
(esfera na origem de raio r²=2)
 até z=1, e de z=1 até
até z=1, e de z=1 até 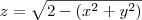
 e
e 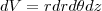 e
e 

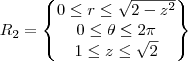
 então se isolar o r temos que
então se isolar o r temos que 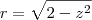 e verificamos que é verdade, pois em z=1, temos que o r=1 pois estamos na fronteira entre os dois sólidos que é a circunferência de raio r=1, e
e verificamos que é verdade, pois em z=1, temos que o r=1 pois estamos na fronteira entre os dois sólidos que é a circunferência de raio r=1, e  temos que r=0, pois é o máximo da região R2, agora que achamos R1 e R2 vamos montar a integral I dividida entre duas regiões:
temos que r=0, pois é o máximo da região R2, agora que achamos R1 e R2 vamos montar a integral I dividida entre duas regiões: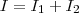
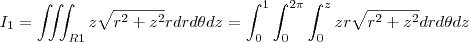
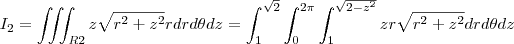
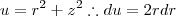 e de forma análoga para a variável z.
e de forma análoga para a variável z.





