Poderiam me ajudar por favor? A questão é a seguinte:
Calcule a integral:
![{I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV {I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV](/latexrender/pictures/db5b81b4fc0f561bab447ff493098c67.png)
Onde R é a região limitada por:
![z = \sqrt[]{2 - {x}^{2} - {y}^{2}} z = \sqrt[]{2 - {x}^{2} - {y}^{2}}](/latexrender/pictures/e1128b31491a40f553d7021da41db36f.png)
e
![z = \sqrt[]{{x}^{2} + {y}^{2}} z = \sqrt[]{{x}^{2} + {y}^{2}}](/latexrender/pictures/593fda6c93daf33d4379ead6624bbe20.png)
Tentei utilizar coordenadas esféricas, mas obtive uma coisa muito complicada de se resolver. Alguém saberia resolver esta questão?

![{I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV {I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV](/latexrender/pictures/db5b81b4fc0f561bab447ff493098c67.png)
![z = \sqrt[]{2 - {x}^{2} - {y}^{2}} z = \sqrt[]{2 - {x}^{2} - {y}^{2}}](/latexrender/pictures/e1128b31491a40f553d7021da41db36f.png)
![z = \sqrt[]{{x}^{2} + {y}^{2}} z = \sqrt[]{{x}^{2} + {y}^{2}}](/latexrender/pictures/593fda6c93daf33d4379ead6624bbe20.png)


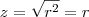
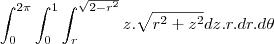


 (cone)
(cone)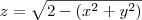 (esfera na origem de raio r²=2)
(esfera na origem de raio r²=2)
 até z=1, e de z=1 até
até z=1, e de z=1 até 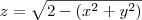
 e
e 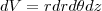 e
e 

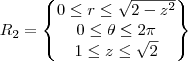
 então se isolar o r temos que
então se isolar o r temos que 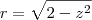 e verificamos que é verdade, pois em z=1, temos que o r=1 pois estamos na fronteira entre os dois sólidos que é a circunferência de raio r=1, e
e verificamos que é verdade, pois em z=1, temos que o r=1 pois estamos na fronteira entre os dois sólidos que é a circunferência de raio r=1, e  temos que r=0, pois é o máximo da região R2, agora que achamos R1 e R2 vamos montar a integral I dividida entre duas regiões:
temos que r=0, pois é o máximo da região R2, agora que achamos R1 e R2 vamos montar a integral I dividida entre duas regiões: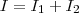
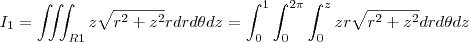
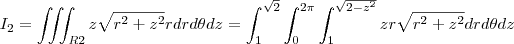
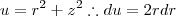 e de forma análoga para a variável z.
e de forma análoga para a variável z.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.