 por livia02 » Sáb Ago 17, 2013 19:29
por livia02 » Sáb Ago 17, 2013 19:29
Estava acompanhando uma explicação no livro da resolução de uma equação diferencial e não entendi um passo da resolução:
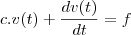
(lembrando que c e f são números)
1º - Fazendo
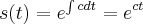
e multiplicando os dois lados da equação temos:
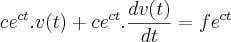
2º - Depois ele substitui
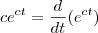
.
Não entendi esses dois passos. Da onde ele tirou
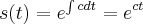
? Como ele chegou a esse valor para substituir? E no segundo passos, porque ele substituiu pela derivada?
Alguém pode me explicar o porque desses passos?
Obrigada!
-
livia02
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Ago 14, 2013 20:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia mecânica
- Andamento: cursando
 por MateusL » Sáb Ago 17, 2013 23:36
por MateusL » Sáb Ago 17, 2013 23:36
Acho que ele fez tudo isso para poder escrever o lado esquerdo da equação como a derivada de um produto de funções.
Então, ele criou uma função
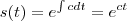
para que
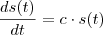
.
Então, multiplicando os dois lados por
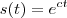
:
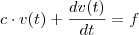
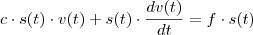
Como
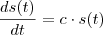
, podemos escrever que:
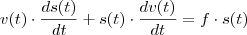
Pela derivada do produto,
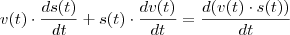
, então:
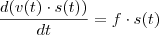
Espero que seja isso.
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral por substituição / Integral por partes
por Carlos28 » Seg Out 19, 2015 12:25
- 1 Respostas
- 3039 Exibições
- Última mensagem por nakagumahissao

Seg Out 19, 2015 23:26
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Substituição
por Aliocha Karamazov » Qui Fev 23, 2012 23:57
- 2 Respostas
- 2457 Exibições
- Última mensagem por MarceloFantini

Sex Fev 24, 2012 12:07
Cálculo: Limites, Derivadas e Integrais
-
- Integral (substituição)
por kika_sanches » Sex Mar 23, 2012 14:42
- 4 Respostas
- 3128 Exibições
- Última mensagem por kika_sanches

Sex Mar 23, 2012 15:35
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao (u.du)
por menino de ouro » Dom Nov 18, 2012 10:46
- 1 Respostas
- 1827 Exibições
- Última mensagem por young_jedi

Dom Nov 18, 2012 10:54
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao (u.du)
por menino de ouro » Seg Nov 19, 2012 16:23
- 7 Respostas
- 4602 Exibições
- Última mensagem por MarceloFantini

Ter Nov 20, 2012 21:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
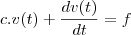 (lembrando que c e f são números)
(lembrando que c e f são números)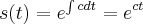 e multiplicando os dois lados da equação temos:
e multiplicando os dois lados da equação temos: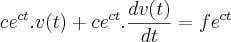
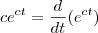 .
.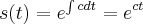 ? Como ele chegou a esse valor para substituir? E no segundo passos, porque ele substituiu pela derivada?
? Como ele chegou a esse valor para substituir? E no segundo passos, porque ele substituiu pela derivada?

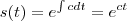 para que
para que 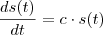 .
.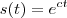 :
: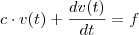
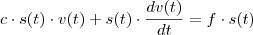
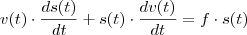
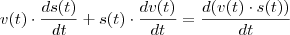 , então:
, então: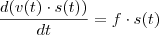

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.