Analisando a figura anexada , não sei você observou , mas o segmento

é perpendicular a

e portanto constitui uma altura do triângulo retângulo ABC relativa a base BC . Designando
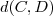
a distância do ponto C até o ponto D , temos que a área deste triângulo retângulo (que é 36 unidades de área ) será dada por :

(1) . E como determinar o ponto C ?
Te dou uma dica para concluir , os pontos A,B,C são colineares , então determinado a equação da reta pelos pontos A, B dados você determinar o ponto C .
Outra forma mais simples (ou talvez não ).
Seja

o ângulo entre o segmento BC e BD (note também que tal ângulo é a inclinação da reta que passa por A,B [/tex] ) . Por trigonometria ,
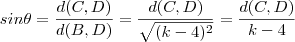
.
Além disso ,
o coeficiente angular da reta que passa pelos pontos A,B é dado por :
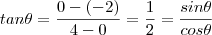
Logo ,
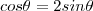
Elevando ambos membro ao quadrado e utilizando a identidade trigonométrica fundamental
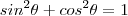
temos :
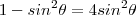
Resolvendo a eq. do segundo grau para

obteremos a distancia do ponto C a D que é :

e portanto pela equação (1) encontraremos k que satisfaça a igualdade ..Espero que ajude .


 é perpendicular a
é perpendicular a  e portanto constitui uma altura do triângulo retângulo ABC relativa a base BC . Designando
e portanto constitui uma altura do triângulo retângulo ABC relativa a base BC . Designando 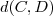 a distância do ponto C até o ponto D , temos que a área deste triângulo retângulo (que é 36 unidades de área ) será dada por :
a distância do ponto C até o ponto D , temos que a área deste triângulo retângulo (que é 36 unidades de área ) será dada por :  (1) . E como determinar o ponto C ?
(1) . E como determinar o ponto C ? o ângulo entre o segmento BC e BD (note também que tal ângulo é a inclinação da reta que passa por A,B [/tex] ) . Por trigonometria ,
o ângulo entre o segmento BC e BD (note também que tal ângulo é a inclinação da reta que passa por A,B [/tex] ) . Por trigonometria , 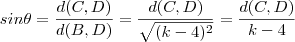 .
.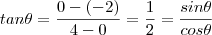
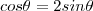
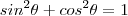 temos :
temos : 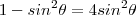
 obteremos a distancia do ponto C a D que é :
obteremos a distancia do ponto C a D que é : 

 .
. ?
? e
e ![d(B,C)= \sqrt[2]{29} d(B,C)= \sqrt[2]{29}](/latexrender/pictures/77e0b43a90d3d0fbbde3bef205aeb125.png) . Está certo isso?
. Está certo isso?

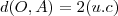 e
e 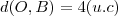 obtemos que :
obtemos que :  .
.  ,obtendo
,obtendo ![[d(C,D)]^2 = 36 [d(C,D)]^2 = 36](/latexrender/pictures/851e88a6014fed4340d659e4fe35a255.png) e portanto
e portanto  . Daí ,
. Daí ,  . Agora pelo terorema de Pitágoras ,
. Agora pelo terorema de Pitágoras ,  . Tente concluir a parti daqui .
. Tente concluir a parti daqui .  corresponde a eq. da reta que passa pelos pontos A,B (está correto verifiquei ) . Em relação ao ponto (1,-2) ,ele não pertence a reta em questão . Pois as coordenadas deste ponto não satisfaz a eq. desta reta ,
corresponde a eq. da reta que passa pelos pontos A,B (está correto verifiquei ) . Em relação ao ponto (1,-2) ,ele não pertence a reta em questão . Pois as coordenadas deste ponto não satisfaz a eq. desta reta , 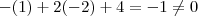 ,logo descartamos a possibilidade do ponto C ser ele .
,logo descartamos a possibilidade do ponto C ser ele .![d(B,D) = \sqrt[]{210} d(B,D) = \sqrt[]{210}](/latexrender/pictures/910a1082ce44183475eab1fa469dc9e6.png) .
.![{d(B,D)}^{2} = {(Xd - Xb)}^{2}+ {(Yd - Yb)}^{2}
{d(B,D)}^{2} = {(K-4)}^{2} + {(0-0)}^{2}
{(\sqrt[]{210})^{2} = {(K-4)}^{2}
210 = {K}^{2} -8K + 16
{K}^{2} - 8K - 194 = 0 {d(B,D)}^{2} = {(Xd - Xb)}^{2}+ {(Yd - Yb)}^{2}
{d(B,D)}^{2} = {(K-4)}^{2} + {(0-0)}^{2}
{(\sqrt[]{210})^{2} = {(K-4)}^{2}
210 = {K}^{2} -8K + 16
{K}^{2} - 8K - 194 = 0](/latexrender/pictures/b8fd2c0c482a68bee7f25073c0202f37.png)
![k' = 8 + 2 \sqrt[]{210}/2
k'' = 8 - 2 \sqrt[]{210}/2. k' = 8 + 2 \sqrt[]{210}/2
k'' = 8 - 2 \sqrt[]{210}/2.](/latexrender/pictures/5ec0d6550cc1ad7a4bb3250e0a6c77bc.png)
![\sqrt[]{210} \sqrt[]{210}](/latexrender/pictures/ab3294cdbb5af6bf292bd5c166e836eb.png) gostou tanto da minha burrice que resolver ficar aí, rindo da minha cara ( piadinha sem-graça eu sei kkk).
gostou tanto da minha burrice que resolver ficar aí, rindo da minha cara ( piadinha sem-graça eu sei kkk).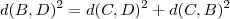 (Esta igualdade decorre do Teorema de Pitágoras ) . Segue ,
(Esta igualdade decorre do Teorema de Pitágoras ) . Segue , ![d(B,D)^2 = d(C,D)^2+ [2d(C,D)]^2 =d(C,D)^2+ 4d(C,D)^2 = 5 d(C,D)^2 d(B,D)^2 = d(C,D)^2+ [2d(C,D)]^2 =d(C,D)^2+ 4d(C,D)^2 = 5 d(C,D)^2](/latexrender/pictures/a8a95cce5229f9095a50733a59d3bbd6.png) .
. 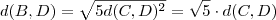 .
. 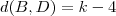 (porque ? ) . Então :
(porque ? ) . Então : 
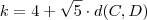 .Lembrando que
.Lembrando que  (revise o tópico que encontramos este resultado ) obtemos finalmente
(revise o tópico que encontramos este resultado ) obtemos finalmente 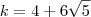 .
.