 por Flordelis25 » Sex Ago 02, 2013 19:29
por Flordelis25 » Sex Ago 02, 2013 19:29
Oi pessoal (:
Bom já tentei achar o k, mas minha resposta não bate com a do gabarito que é 4 + 6?5
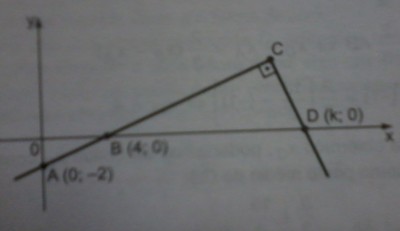
Na figura a seguir, os pontos A,B e C são colineares. Determine o valor de k sabendo que a área do triângulo BCD é 36.
A imagem do exercício está em anexo.
Obrigada (:
- Anexos
-
-
Flordelis25
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Abr 20, 2013 17:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Sex Ago 02, 2013 22:44
por e8group » Sex Ago 02, 2013 22:44
Analisando a figura anexada , não sei você observou , mas o segmento

é perpendicular a

e portanto constitui uma altura do triângulo retângulo ABC relativa a base BC . Designando
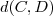
a distância do ponto C até o ponto D , temos que a área deste triângulo retângulo (que é 36 unidades de área ) será dada por :

(1) . E como determinar o ponto C ?
Te dou uma dica para concluir , os pontos A,B,C são colineares , então determinado a equação da reta pelos pontos A, B dados você determinar o ponto C .
Outra forma mais simples (ou talvez não ).
Seja

o ângulo entre o segmento BC e BD (note também que tal ângulo é a inclinação da reta que passa por A,B [/tex] ) . Por trigonometria ,
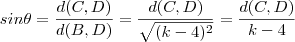
.
Além disso ,
o coeficiente angular da reta que passa pelos pontos A,B é dado por :
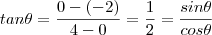
Logo ,
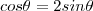
Elevando ambos membro ao quadrado e utilizando a identidade trigonométrica fundamental
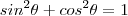
temos :
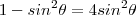
Resolvendo a eq. do segundo grau para

obteremos a distancia do ponto C a D que é :

e portanto pela equação (1) encontraremos k que satisfaça a igualdade ..Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Flordelis25 » Sáb Ago 03, 2013 21:53
por Flordelis25 » Sáb Ago 03, 2013 21:53
santhiago escreveu:Analisando a figura anexada , não sei você observou , mas o segmento

é perpendicular a

e portanto constitui uma altura do triângulo retângulo ABC relativa a base BC . Designando
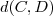
a distância do ponto C até o ponto D , temos que a área deste triângulo retângulo (que é 36 unidades de área ) será dada por :

(1) . E como determinar o ponto C ?
Te dou uma dica para concluir , os pontos A,B,C são colineares , então determinado a equação da reta pelos pontos A, B dados você determinar o ponto C .
Outra forma mais simples (ou talvez não ).
Seja

o ângulo entre o segmento BC e BD (note também que tal ângulo é a inclinação da reta que passa por A,B [/tex] ) . Por trigonometria ,
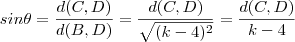
.
Além disso ,
o coeficiente angular da reta que passa pelos pontos A,B é dado por :
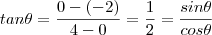
Logo ,
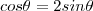
Elevando ambos membro ao quadrado e utilizando a identidade trigonométrica fundamental
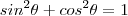
temos :
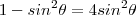
Resolvendo a eq. do segundo grau para

obteremos a distancia do ponto C a D que é :

e portanto pela equação (1) encontraremos k que satisfaça a igualdade ..Espero que ajude .
Santhiago, seguinte. Fiz o que vc disse, usei o primeiro método, para mim o mais fácil. Utilizando os pontos A e B, por determinante achei a equação

.
O ponto C seria

?
Tentei resolver por esse ponto, a distência

e
![d(B,C)= \sqrt[2]{29} d(B,C)= \sqrt[2]{29}](/latexrender/pictures/77e0b43a90d3d0fbbde3bef205aeb125.png)
. Está certo isso?
Obrigada pela ajuda

-
Flordelis25
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Abr 20, 2013 17:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Sáb Ago 03, 2013 23:47
por e8group » Sáb Ago 03, 2013 23:47
Avaliarei sua resposta a seguir .Entretanto vale ressaltar que há uma forma mais simples de resolver este exercício .Já notou que os triângulos retângulos OAB e CBD são semelhantes ? Pois bem , podemos usar então que

Sendo
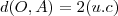
e
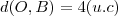
obtemos que :

.
Podemos substituir este resultado na expressão que fornece a área do triângulo retângulo CBD que é

,obtendo
![[d(C,D)]^2 = 36 [d(C,D)]^2 = 36](/latexrender/pictures/851e88a6014fed4340d659e4fe35a255.png)
e portanto

. Daí ,

. Agora pelo terorema de Pitágoras ,

. Tente concluir a parti daqui .
Respondendo a sua resposta agora .
A equação que você encontrou

corresponde a eq. da reta que passa pelos pontos A,B (está correto verifiquei ) . Em relação ao ponto (1,-2) ,ele não pertence a reta em questão . Pois as coordenadas deste ponto não satisfaz a eq. desta reta ,
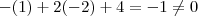
,logo descartamos a possibilidade do ponto C ser ele .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Flordelis25 » Seg Ago 05, 2013 21:39
por Flordelis25 » Seg Ago 05, 2013 21:39
Olá Santhiago! Como tem passado?
Eu tinha pensando nesse jeito por semelhança de triângulo, mas estava com receio de usá-lo. Bem, a questão é que eu fiz o que vc disse. Terminei Pitágoras e achei que
![d(B,D) = \sqrt[]{210} d(B,D) = \sqrt[]{210}](/latexrender/pictures/910a1082ce44183475eab1fa469dc9e6.png)
.
Ok, até aí tudo bem. Joguei na fórmula da distância e achei que:
![{d(B,D)}^{2} = {(Xd - Xb)}^{2}+ {(Yd - Yb)}^{2}
{d(B,D)}^{2} = {(K-4)}^{2} + {(0-0)}^{2}
{(\sqrt[]{210})^{2} = {(K-4)}^{2}
210 = {K}^{2} -8K + 16
{K}^{2} - 8K - 194 = 0 {d(B,D)}^{2} = {(Xd - Xb)}^{2}+ {(Yd - Yb)}^{2}
{d(B,D)}^{2} = {(K-4)}^{2} + {(0-0)}^{2}
{(\sqrt[]{210})^{2} = {(K-4)}^{2}
210 = {K}^{2} -8K + 16
{K}^{2} - 8K - 194 = 0](/latexrender/pictures/b8fd2c0c482a68bee7f25073c0202f37.png)
Ok, eis que \Delta = 840. Então fiz Bhaskara só que está dando
![k' = 8 + 2 \sqrt[]{210}/2
k'' = 8 - 2 \sqrt[]{210}/2. k' = 8 + 2 \sqrt[]{210}/2
k'' = 8 - 2 \sqrt[]{210}/2.](/latexrender/pictures/5ec0d6550cc1ad7a4bb3250e0a6c77bc.png)
Agora ou eu fiz uma coisa muito errada ou essa
![\sqrt[]{210} \sqrt[]{210}](/latexrender/pictures/ab3294cdbb5af6bf292bd5c166e836eb.png)
gostou tanto da minha burrice que resolver ficar aí, rindo da minha cara ( piadinha sem-graça eu sei kkk).
Falando sério, o que eu fiz de errado? Já estou ficando louca com esse exercício que estou pensando seriamente em abolir a letra k do meu alfabeto.
Agradeço desde já e desculpa por tomar seu tempo.

-
Flordelis25
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Abr 20, 2013 17:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Seg Ago 05, 2013 22:00
por e8group » Seg Ago 05, 2013 22:00
Tudo certo . Na verdade é falta de prática mas não desista ! Observe ,

(lembra que obtemos este resultado por semelhança de triângulos )
Substituindo o resultado acima em ,
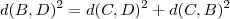
(Esta igualdade decorre do Teorema de Pitágoras ) . Segue ,
![d(B,D)^2 = d(C,D)^2+ [2d(C,D)]^2 =d(C,D)^2+ 4d(C,D)^2 = 5 d(C,D)^2 d(B,D)^2 = d(C,D)^2+ [2d(C,D)]^2 =d(C,D)^2+ 4d(C,D)^2 = 5 d(C,D)^2](/latexrender/pictures/a8a95cce5229f9095a50733a59d3bbd6.png)
.
Assim ,
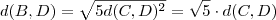
.
Por outro lado ,
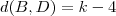
(porque ? ) . Então :

e portanto :
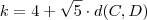
.Lembrando que

(revise o tópico que encontramos este resultado ) obtemos finalmente
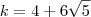
.
OBS.: Recomendo que refaça este exercício para aprender a desenvolver .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Flordelis25 » Ter Ago 06, 2013 18:04
por Flordelis25 » Ter Ago 06, 2013 18:04
Hummm entendi. Eu não poderia ter feito direto. Tinha que ter "simplificado" mais.
Vou refazer esse exercício de novo, sem olhar a resolução para ver se peguei o raciocínio. Sabe como é, quando se estuda para o vestibular, matemática se torna o pesadelo rsrsr
De qualquer forma, obrigada mesmo pela ajuda Santhiago e desculpa ter tomado seu tempo com minhas perguntas, mas o professor do meu cursinho complica demais as coisas.
Obrigada mais uma vez

-
Flordelis25
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Abr 20, 2013 17:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- como eu acho a taxa
por weverton » Qui Mai 20, 2010 03:12
- 6 Respostas
- 7075 Exibições
- Última mensagem por weverton

Qua Jun 23, 2010 17:48
Matemática Financeira
-
- Como eu acho os ângulos
por Balanar » Qua Set 01, 2010 01:04
- 5 Respostas
- 4751 Exibições
- Última mensagem por ednaldo1982

Sex Mar 30, 2012 00:46
Geometria Plana
-
- [Escalonamento de matrizes] Como acho C^-1
por Ronaldobb » Qui Abr 25, 2013 12:38
- 1 Respostas
- 1878 Exibições
- Última mensagem por DanielFerreira

Qui Abr 25, 2013 19:18
Álgebra Linear
-
- Como eu acho os fatores primos de um número?
por Antony Shuazter » Seg Jun 18, 2012 09:40
- 5 Respostas
- 4115 Exibições
- Última mensagem por Antony Shuazter

Ter Jun 19, 2012 23:22
Sistemas de Equações
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7170 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 é perpendicular a
é perpendicular a  e portanto constitui uma altura do triângulo retângulo ABC relativa a base BC . Designando
e portanto constitui uma altura do triângulo retângulo ABC relativa a base BC . Designando 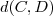 a distância do ponto C até o ponto D , temos que a área deste triângulo retângulo (que é 36 unidades de área ) será dada por :
a distância do ponto C até o ponto D , temos que a área deste triângulo retângulo (que é 36 unidades de área ) será dada por :  (1) . E como determinar o ponto C ?
(1) . E como determinar o ponto C ? o ângulo entre o segmento BC e BD (note também que tal ângulo é a inclinação da reta que passa por A,B [/tex] ) . Por trigonometria ,
o ângulo entre o segmento BC e BD (note também que tal ângulo é a inclinação da reta que passa por A,B [/tex] ) . Por trigonometria , 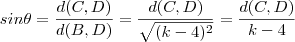 .
.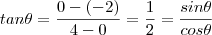
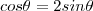
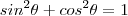 temos :
temos : 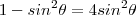
 obteremos a distancia do ponto C a D que é :
obteremos a distancia do ponto C a D que é : 

 .
. ?
? e
e ![d(B,C)= \sqrt[2]{29} d(B,C)= \sqrt[2]{29}](/latexrender/pictures/77e0b43a90d3d0fbbde3bef205aeb125.png) . Está certo isso?
. Está certo isso?

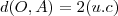 e
e 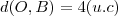 obtemos que :
obtemos que :  .
.  ,obtendo
,obtendo ![[d(C,D)]^2 = 36 [d(C,D)]^2 = 36](/latexrender/pictures/851e88a6014fed4340d659e4fe35a255.png) e portanto
e portanto  . Daí ,
. Daí ,  . Agora pelo terorema de Pitágoras ,
. Agora pelo terorema de Pitágoras ,  . Tente concluir a parti daqui .
. Tente concluir a parti daqui .  corresponde a eq. da reta que passa pelos pontos A,B (está correto verifiquei ) . Em relação ao ponto (1,-2) ,ele não pertence a reta em questão . Pois as coordenadas deste ponto não satisfaz a eq. desta reta ,
corresponde a eq. da reta que passa pelos pontos A,B (está correto verifiquei ) . Em relação ao ponto (1,-2) ,ele não pertence a reta em questão . Pois as coordenadas deste ponto não satisfaz a eq. desta reta , 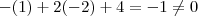 ,logo descartamos a possibilidade do ponto C ser ele .
,logo descartamos a possibilidade do ponto C ser ele .![d(B,D) = \sqrt[]{210} d(B,D) = \sqrt[]{210}](/latexrender/pictures/910a1082ce44183475eab1fa469dc9e6.png) .
.![{d(B,D)}^{2} = {(Xd - Xb)}^{2}+ {(Yd - Yb)}^{2}
{d(B,D)}^{2} = {(K-4)}^{2} + {(0-0)}^{2}
{(\sqrt[]{210})^{2} = {(K-4)}^{2}
210 = {K}^{2} -8K + 16
{K}^{2} - 8K - 194 = 0 {d(B,D)}^{2} = {(Xd - Xb)}^{2}+ {(Yd - Yb)}^{2}
{d(B,D)}^{2} = {(K-4)}^{2} + {(0-0)}^{2}
{(\sqrt[]{210})^{2} = {(K-4)}^{2}
210 = {K}^{2} -8K + 16
{K}^{2} - 8K - 194 = 0](/latexrender/pictures/b8fd2c0c482a68bee7f25073c0202f37.png)
![k' = 8 + 2 \sqrt[]{210}/2
k'' = 8 - 2 \sqrt[]{210}/2. k' = 8 + 2 \sqrt[]{210}/2
k'' = 8 - 2 \sqrt[]{210}/2.](/latexrender/pictures/5ec0d6550cc1ad7a4bb3250e0a6c77bc.png)
![\sqrt[]{210} \sqrt[]{210}](/latexrender/pictures/ab3294cdbb5af6bf292bd5c166e836eb.png) gostou tanto da minha burrice que resolver ficar aí, rindo da minha cara ( piadinha sem-graça eu sei kkk).
gostou tanto da minha burrice que resolver ficar aí, rindo da minha cara ( piadinha sem-graça eu sei kkk).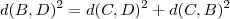 (Esta igualdade decorre do Teorema de Pitágoras ) . Segue ,
(Esta igualdade decorre do Teorema de Pitágoras ) . Segue , ![d(B,D)^2 = d(C,D)^2+ [2d(C,D)]^2 =d(C,D)^2+ 4d(C,D)^2 = 5 d(C,D)^2 d(B,D)^2 = d(C,D)^2+ [2d(C,D)]^2 =d(C,D)^2+ 4d(C,D)^2 = 5 d(C,D)^2](/latexrender/pictures/a8a95cce5229f9095a50733a59d3bbd6.png) .
. 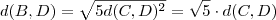 .
. 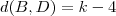 (porque ? ) . Então :
(porque ? ) . Então : 
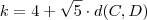 .Lembrando que
.Lembrando que  (revise o tópico que encontramos este resultado ) obtemos finalmente
(revise o tópico que encontramos este resultado ) obtemos finalmente 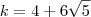 .
.