Vou tentar responder de forma generalizada .
Considere a matriz

e
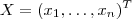
solução do sistema linear homogêneo
![(*) A \cdot X =[O_{\mathbb{R} ^n} ] ^T = (0,\hdots , 0 )^T (*) A \cdot X =[O_{\mathbb{R} ^n} ] ^T = (0,\hdots , 0 )^T](/latexrender/pictures/0aac13c5272ed6f77a734e8d55621c83.png)
.Suponhamos que após aplicarmos operações elementares

na matriz

obtemos a matriz identidade

.Ora ,neste caso a matriz

é equivalente por linhas a matriz identidade

,logo o sistema

é compatível e determinado e portanto a matriz

é invertível .
Uma demonstração (não tenho certeza se está correta )
Vamos denotar

as matrizes elementares obtidas respectivamente pelas operações elementares

sobre a matriz identidade .
A demonstração é simples , podemos escrever
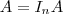
certo ? Aplicando a operação elementar
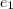
em ambos membros , temos
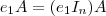
[observe que tal operação pode ser por exemplo : multiplicar a primeira linha da matriz identidade por um número e somar a segunda linha] ,de forma análoga se obtêm
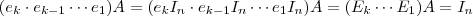

Portanto

é invertível e sua inversa é

a qual denotaremos por

.
Agora vejamos um método para verificar se uma determinada matriz é invertível .
Se

é invertível então

, logo

,caso

não fosse invertível segue
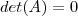
.
Conclusão : Podemos verificar se o sistema(*) possui solução além da trivial se
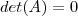
.
Pois se
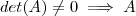
invertível e portanto multiplicando-se pela esquerda ambos membros de (*) por

, temos :

e é fácil verificar a unicidade .
Resumindo : Um sistema linear

é compatível e determinado se

caso contrário este sistema pode ser compatível e indeterminado ou incompatível (não há solução ) .
![Det{\left[T \right]}_{nxn} Det{\left[T \right]}_{nxn}](/latexrender/pictures/9564952a3b243fde557bb39521d76f82.png) for igual a zero em um sistema linear homogêneo, o sistema admite não somente a solução trivial, e que se o determinante for igual a zero, o sistema só admite a solução trivial.
for igual a zero em um sistema linear homogêneo, o sistema admite não somente a solução trivial, e que se o determinante for igual a zero, o sistema só admite a solução trivial.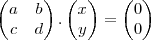
 então a solução do sistema é não somente a solução trivial.
então a solução do sistema é não somente a solução trivial.

 e
e 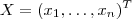 solução do sistema linear homogêneo
solução do sistema linear homogêneo ![(*) A \cdot X =[O_{\mathbb{R} ^n} ] ^T = (0,\hdots , 0 )^T (*) A \cdot X =[O_{\mathbb{R} ^n} ] ^T = (0,\hdots , 0 )^T](/latexrender/pictures/0aac13c5272ed6f77a734e8d55621c83.png) .Suponhamos que após aplicarmos operações elementares
.Suponhamos que após aplicarmos operações elementares  na matriz
na matriz  obtemos a matriz identidade
obtemos a matriz identidade  .Ora ,neste caso a matriz
.Ora ,neste caso a matriz  é compatível e determinado e portanto a matriz
é compatível e determinado e portanto a matriz  as matrizes elementares obtidas respectivamente pelas operações elementares
as matrizes elementares obtidas respectivamente pelas operações elementares 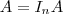 certo ? Aplicando a operação elementar
certo ? Aplicando a operação elementar 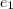 em ambos membros , temos
em ambos membros , temos 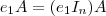 [observe que tal operação pode ser por exemplo : multiplicar a primeira linha da matriz identidade por um número e somar a segunda linha] ,de forma análoga se obtêm
[observe que tal operação pode ser por exemplo : multiplicar a primeira linha da matriz identidade por um número e somar a segunda linha] ,de forma análoga se obtêm 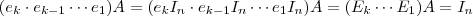

 a qual denotaremos por
a qual denotaremos por  .
. , logo
, logo  ,caso
,caso 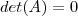 .
.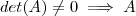 invertível e portanto multiplicando-se pela esquerda ambos membros de (*) por
invertível e portanto multiplicando-se pela esquerda ambos membros de (*) por 
 é compatível e determinado se
é compatível e determinado se  caso contrário este sistema pode ser compatível e indeterminado ou incompatível (não há solução ) .
caso contrário este sistema pode ser compatível e indeterminado ou incompatível (não há solução ) .
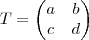
 tal que ax+by=0, então qualquer vetor paralelo a
tal que ax+by=0, então qualquer vetor paralelo a  tb te leva a 0. Mas qualquer matriz com uma linha ou coluna paralela a outra forma um conjunto LD e, portanto, tem determinante nulo. Logo, existem infinitas soluções para o sistema. Por outro lado, se a matriz tem posto completo, então o conjunto é LI e, portanto, os vetores que a formam não serão paralelos. Então, a única solução possível é a trivial.
tb te leva a 0. Mas qualquer matriz com uma linha ou coluna paralela a outra forma um conjunto LD e, portanto, tem determinante nulo. Logo, existem infinitas soluções para o sistema. Por outro lado, se a matriz tem posto completo, então o conjunto é LI e, portanto, os vetores que a formam não serão paralelos. Então, a única solução possível é a trivial.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.