Fala pessoal
Estou com dúvida em uma questão. A resposta é P(1,0,0), consegui até entender o raciocínio mas queria saber como fazer a questão "na tora", desenvolvendo tudo certinho.
Sejam:
A(1,1,1)
B(0,0,1)
r: X = (1,0,0) + t(1,1,1)
Determine os pontos de r equidistantes de A e B:


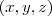 até o ponto
até o ponto  é:
é:
 :
:



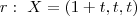
 , teremos
, teremos  e
e  .
.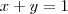
 , portanto, o ponto procurado é
, portanto, o ponto procurado é  .
.