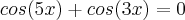
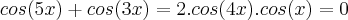
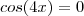
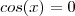
Daí cheguei na seguinte solução:
S = {x e R| x = pi/2 + k.pi ou x = pi/8 + k.pi/4, k e Z}
Enfim, gostaria de saber se tem uma outra forma de resolver essa equação.
por Rafael16 » Ter Jul 23, 2013 17:51
por MateusL » Qua Jul 24, 2013 15:46
por Rafael16 » Qua Jul 24, 2013 16:15
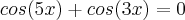
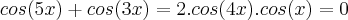
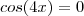
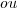
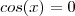
MateusL escreveu:Olá!
Acredito que essa seja uma das formas mais simples de resolver.
Todas as outras formas que consegui pensar não são tão simples como essa.
Abraço!
por MateusL » Qui Jul 25, 2013 17:51
Rafael16 escreveu:Obrigado MateusL!
Estava pensando dessa maneira:
cos(a) = cos(b) --> a = b + 2k.pi ou a = - b + 2k.pi
Só que dessa maneira não iria da certo por causa do sinal negativo (cos 5x = - cos 3x). Certo?
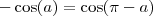, então obterías 
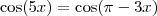. Até cheguei a pensar em algo do tipo, mas, à primeira vista, me pareceu que daria mais trabalho, mas realmente fica mais simples: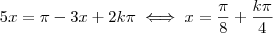
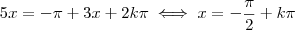
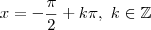, apesar de estar escrito de maneira diferente, é uma solução equivalente a 
.
por Ananda » Sex Mar 14, 2008 22:37
por renataf » Sex Dez 03, 2010 11:06
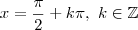Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)