[Integral] Integral de "função implícita"

por **mthc10** » Qua Jul 24, 2013 01:08

Olá amigos, Boas,
Bom estou com um problema... Estou estudando pelo livro Leithold e fazendo seus respectivos exercícios, porém há algumas questão que eu não consigo resolver, e nem o livro soluciona questões semelhantes para eu ter noção de como resolver, e por isso peço a ajuda de vocês!

A questão é a seguinte:

"Ache a área da região limitada pela reta x=4

e pela curva x^3 -x^2 +2xy -y^2 = 0

."

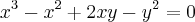O livro apresenta uma sugestão para resolver tal problema, que seria o seguinte: "resolva a equação cúbica em y em termos de x e expresse y como duas funções de x.".
Bom, não consigo isolar X e Y dessa "função". Então não me ajudou muito tal sugestão.

O que eu (acho que)entendi é que para resolver esse problema, terei de achar os pontos onde essa curva intercepta a reta x = 4 e integrar essa curva sendo os limites de integração 0 e 4, visto que se x=0, y=0.
Alguém pode ajudar ? Obrigado desde já!

por **Russman** » Qua Jul 24, 2013 01:36

A curva mencionada não esta na forma y = f(x)

. Portanto, você deve tentar colocá-la assim. Para isto, visto que a forma implícita é uma forma cúbica em

você deve tentar resolvê-la para

ou resolvê-la para

percebendo que ela é uma forma quadática para

. Na primeira, você obterá y=f(x)

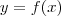e na segunda x = f(y)

.

Repare que

x^3 - x^2 + 2xy - y^2 = x^3 -(x-y)^2

de modo que

$x^3 - (x-y)^2 = 0 \Rightarrow x^3 = (x-y)^2 \Rightarrow \left\{\begin{matrix} x^{\frac{3}{2}} = x-y \Rightarrow y=x - x^{\frac{3}{2}}\\ x^{\frac{3}{2}} = -x+y \Rightarrow y=x + x^{\frac{3}{2}} \end{matrix}\right.$

e temos duas soluções possíveis para

.

O gráfico dessas funções é

: graph; graph (3).gif (5.66 KiB) Exibido 2591 vezes

de modo que a área delimitada por elas é bem visível. Eu acho que você terá de calcular a área da curva de cima de x=0

até

e descontar da área da curva de baixo no mesmo intervalo. Descontar sim, pq de x=0

até

a curva de baixo tem área positiva e em diante tem area negativa via integral. Daí, como no primeiro intervalo voce deve subtrair da área total e no segundo somar, os sinais se equilibram e voce tem o resultado de imediato.

por **mthc10** » Qua Jul 24, 2013 01:55

Desculpe a ignorância, mas como eu faço isso ?
Essa é a minha dificuldade, já que não consigo isolar as incógnitas... Se não consigo isolar as incógnitas, como vou resolver a equação em y ou em x ?

por **mthc10** » Qua Jul 24, 2013 13:02

Amigo, obrigado, consegui resolver graças a você!
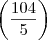É sim como você disse, Integral da função de cima $\left( \frac{104}{5} \right)$ - integral da função de baixo $\left( \frac{-24}{5} \right)$ .
Como resultado: $\frac{128}{5}$

Obrigado pela ajuda!

[Integral] Integral de "função implícita"

[Integral] Integral de "função implícita"

[Integral] Integral de "função implícita"

Re: [Integral] Integral de "função implícita"

Re: [Integral] Integral de "função implícita"

Re: [Integral] Integral de "função implícita"

Quem está online