
nesses exercícios aqui não estão conferindo com o gabarito. Alguém poderia por favor identificar onde está o erro? Não consegui terminar sendo que não exite raiz cúbica exata desses números...
Simplifique as raízes cúbicas:
![\sqrt[3]{500}=\sqrt[3]{5.100}=\sqrt[3]{5}.\sqrt[3]{100} \sqrt[3]{500}=\sqrt[3]{5.100}=\sqrt[3]{5}.\sqrt[3]{100}](/latexrender/pictures/61cf7b07d963be9d06b79cc65f7f86ee.png)
![\sqrt[3]{320}=\sqrt[3]{4.80}=\sqrt[3]{4}.\sqrt[3]{80} \sqrt[3]{320}=\sqrt[3]{4.80}=\sqrt[3]{4}.\sqrt[3]{80}](/latexrender/pictures/bde66e5ad42a7bd74aced09d9293bdc8.png)
![\sqrt[3]{-81}=\sqrt[3]{9.-9}=\sqrt[3]{3.-3}.\sqrt[3]{3.3}=-3\sqrt[3]{3} \sqrt[3]{-81}=\sqrt[3]{9.-9}=\sqrt[3]{3.-3}.\sqrt[3]{3.3}=-3\sqrt[3]{3}](/latexrender/pictures/26a12544744027db10ba762cd20432b7.png)
Os resultados são respectivamente:
![5\sqrt[3]{3} 5\sqrt[3]{3}](/latexrender/pictures/58a6fc46f0845e880cd6aef6fcb091ab.png) ,
, ![4\sqrt[3]{5} 4\sqrt[3]{5}](/latexrender/pictures/34b5e71191c992181601e356a60830e4.png) ,
, ![-3\sqrt[3]{3} -3\sqrt[3]{3}](/latexrender/pictures/a91e8466260d76b3d991bbd8374b1ad0.png) .
.

![\sqrt[n]a = a^{1/n} \sqrt[n]a = a^{1/n}](/latexrender/pictures/382b36e65d9fcaf8b11080773a78d1f9.png) . Portanto, se vc elevar este número a n, vc terá
. Portanto, se vc elevar este número a n, vc terá 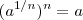
![\sqrt[3]{500} =\sqrt[3]{5^3.4} = 5\sqrt[3]{4} \sqrt[3]{500} =\sqrt[3]{5^3.4} = 5\sqrt[3]{4}](/latexrender/pictures/517f8f1a54af25be5f722c0be52a7ab4.png) (confira o gabarito pra ver se é raiz de 3 ou 4)
(confira o gabarito pra ver se é raiz de 3 ou 4)![\sqrt[3]{420} =\sqrt[3]{4^3.5} = 4\sqrt[3]{5} \sqrt[3]{420} =\sqrt[3]{4^3.5} = 4\sqrt[3]{5}](/latexrender/pictures/27acb069a91dc6681d1aedb01642c964.png)
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)