Seja S={
 } e
} e 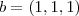 .
.Determine a soma das coordenadas do vetor de S mais próximo de b.
Gabarito:

Desde já, obrigado!

 } e
} e 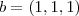 .
.

 do
do  ,mais precisamente ,
,mais precisamente ,  um é subespaço do
um é subespaço do  ,seus vetores são os pontos
,seus vetores são os pontos  que satisfaz a propriedade do conjunto
que satisfaz a propriedade do conjunto  que é
que é 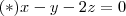 . Indo diretamente a geometria analítica ,seja
. Indo diretamente a geometria analítica ,seja 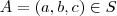 o ponto mais próximo de
o ponto mais próximo de  .Definindo
.Definindo  vetor normal ao plano que passa pela origem de equação
vetor normal ao plano que passa pela origem de equação  e escolhendo um ponto arbitrário
e escolhendo um ponto arbitrário  em
em  (Escolha o ponto que você quiser,fique à vontade !) .
(Escolha o ponto que você quiser,fique à vontade !) . 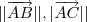 e hipotenusa
e hipotenusa  ,fica fácil ver as seguintes relações :
,fica fácil ver as seguintes relações : 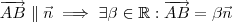

 .
.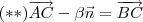 .Multiplicando-se escalarmente
.Multiplicando-se escalarmente  por
por  e usando (b) , segue :
e usando (b) , segue :  .
.  .
.  . Agora já conseguimos obter o ponto
. Agora já conseguimos obter o ponto  ,pois já temos o ponto
,pois já temos o ponto  ,o ponto
,o ponto  e o vetor
e o vetor  .Tente concluir .
.Tente concluir .
santhiago escreveu:Boa tarde .Não verifiquei a resposta ,mas apresentarei um raciocínio para o exercício .O subconjuntodo
,mais precisamente ,
um é subespaço do
,seus vetores são os pontos
que satisfaz a propriedade do conjunto
que é
. Indo diretamente a geometria analítica ,seja
o ponto mais próximo de
.Definindo
vetor normal ao plano que passa pela origem de equação
e escolhendo um ponto arbitrário
em
(Escolha o ponto que você quiser,fique à vontade !) .
Próxima etapa :
Antes de tudo recomendo que faça um esboço da situação . Observando o triângulo retângulo , de catetose hipotenusa
,fica fácil ver as seguintes relações :
(a)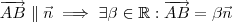
(b)
(c).
Partindo de (c) e usando (a) temos :.Multiplicando-se escalarmente
por
e usando (b) , segue :
.
Logo ,.
Assim , voltando em (a) temos :. Agora já conseguimos obter o ponto
,pois já temos o ponto
,o ponto
e o vetor
.Tente concluir .

santhiago escreveu:Muito bom. Tentarei aplicar o seu raciocínio nesta questão. Mas tendo em vista ser uma questão objetiva e de prova, acredito que haja algo mais simplório para a mesma.
De qualquer modo, muito obrigado Santhiago!

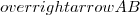 fornece a distância do ponto (1,1,1) ao plano de equação vide propriedade do conjunto S .Como só estamos queremos a soma das coordenadas do ponto A .Vamos verificar :
fornece a distância do ponto (1,1,1) ao plano de equação vide propriedade do conjunto S .Como só estamos queremos a soma das coordenadas do ponto A .Vamos verificar :  .
. temos :
temos : 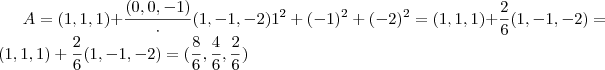
 .
.
santhiago escreveu:Se não cometi nenhum equívoco com o raciocínio o módulo do vetorfornece a distância do ponto (1,1,1) ao plano de equação vide propriedade do conjunto S .Como só estamos queremos a soma das coordenadas do ponto A .Vamos verificar :
.
Escolhendo por exemplotemos :
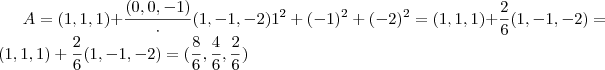
Logo ,.

 é
é 
 tal que:
tal que:
 tal que
tal que 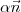 seja igual à projeção ortogonal de
seja igual à projeção ortogonal de 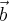 em relação a
em relação a  , pois assim, e somente assim,
, pois assim, e somente assim, 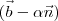 será ortogonal a
será ortogonal a  (em outras palavras, pertencerá a
(em outras palavras, pertencerá a  ), implicando que o produto escalar entre esses dois vetores seja igual a zero.
), implicando que o produto escalar entre esses dois vetores seja igual a zero. , o vetor procurado será
, o vetor procurado será  , que é a projeção de
, que é a projeção de 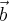 em
em  .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.