Vou ver se consigo.
Queremos encontrar

e

tal que

para todos os valores de

na tabela.
Ou seja, queremos resolver o seguinte sistema:

Seja

,
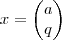
e
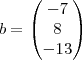
.
Então podemos representar o sistema por
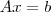
(não confundir este

com o

do enunciado).
Este não é um sistema linear compatível, mas sabemos que a reta que melhor ajusta os dados no sentido dos mínimos quadrados é:
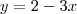
Então

e

, ou seja, a solução pelo método dos mínimos quadrados é

.
É claro que usando estes valores para

, não encontrarás exatamente os valores para

, mas sim os valores que minimizam a soma dos quadrados da diferença entre o valor de

da tabela e o valor de

obtido utilizando este valor de

.
Seja

o subespaço formado pelos vetores-coluna de

.
Queremos encontrar a projeção ortogonal de

sobre

.
Pelo teorema que já postei acima:
... se

é o espaço-coluna de

, então a projeção ortogonal de

em

é:

Então:
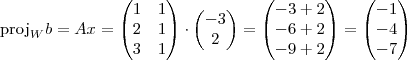
Acredito que seja isso.
Abraço!
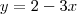 . Usando este fato, determine a projeção ortogonal do vetor
. Usando este fato, determine a projeção ortogonal do vetor 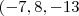 ) sobre
) sobre 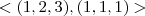 .
.

 é uma matriz
é uma matriz  com vetores-coluna linearmente independentes, então para cada matriz
com vetores-coluna linearmente independentes, então para cada matriz  de tamanho
de tamanho  , o sistema linear
, o sistema linear 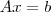 tem uma única solução de mínimos quadrados. Esta solução é dada por:
tem uma única solução de mínimos quadrados. Esta solução é dada por: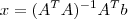
 é o espaço-coluna de
é o espaço-coluna de 
 e
e  tal que
tal que  para todos os valores de
para todos os valores de  na tabela.
na tabela.
 ,
, 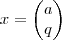 e
e 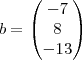 .
.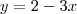
 e
e  , ou seja, a solução pelo método dos mínimos quadrados é
, ou seja, a solução pelo método dos mínimos quadrados é  .
. , mas sim os valores que minimizam a soma dos quadrados da diferença entre o valor de
, mas sim os valores que minimizam a soma dos quadrados da diferença entre o valor de 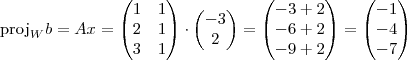
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)