a) A = (1,4), B = (7, -2), R =
![2\sqrt[]{5} 2\sqrt[]{5}](/latexrender/pictures/8afe59aad7560ad383eefaf7fd49cdb9.png) .
.eu tentei fazer criando um sistema com os valores de A e B
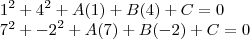
dai descobrindo o valor de "C" com
![R = \sqrt[]{{x}^{2} + {y}^{2} -C} R = \sqrt[]{{x}^{2} + {y}^{2} -C}](/latexrender/pictures/05b7eb94b0bd2edf15b2803031ddfe53.png)
![2\sqrt[]{5} = \sqrt[]{{1}^{2} + {4}^{2} -C} 2\sqrt[]{5} = \sqrt[]{{1}^{2} + {4}^{2} -C}](/latexrender/pictures/bca4b6ebecfa5a6851cf23574b0afeff.png)
mas fiquei por ai.... minha dúvida é, nesse caso as coordenadas A e B correspondem a mesma circunferência, ou cada coordenada corresponde a uma respectiva equação? E, para encontrarmos a equação da circunferência realmente precisamos de 2 coordenadas?
Grato desde já pela compreenção...


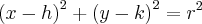
![{(1-h)}^{2}+{(4-k)}^{2}={(2\sqrt[]{5})}^{2} {(1-h)}^{2}+{(4-k)}^{2}={(2\sqrt[]{5})}^{2}](/latexrender/pictures/c7e53ae54b58a205c87f19e47d017147.png)
![{(7-h)}^{2}+{(-2-k)}^{2}={(2\sqrt[]{5})}^{2} {(7-h)}^{2}+{(-2-k)}^{2}={(2\sqrt[]{5})}^{2}](/latexrender/pictures/71251947c4190b39e4b95692fa904478.png)
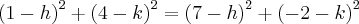
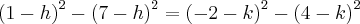



![{(x-3)}^{2}+{(y-0)}^{2}={(2\sqrt[]{5})}^{2} {(x-3)}^{2}+{(y-0)}^{2}={(2\sqrt[]{5})}^{2}](/latexrender/pictures/9a8e30f9c7765893990a178e8f1135c9.png)
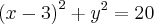

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.