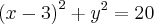por shirata » Qua Nov 11, 2009 20:37
por shirata » Qua Nov 11, 2009 20:37
Obtenha a equação de uma circunferência de raio R e que passa pelos pontos A e B, nos seguintes casos:
a) A = (1,4), B = (7, -2), R =
![2\sqrt[]{5} 2\sqrt[]{5}](/latexrender/pictures/8afe59aad7560ad383eefaf7fd49cdb9.png)
.
eu tentei fazer criando um sistema com os valores de A e B
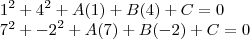 dai descobrindo o valor de "C" com
dai descobrindo o valor de "C" com ![R = \sqrt[]{{x}^{2} + {y}^{2} -C} R = \sqrt[]{{x}^{2} + {y}^{2} -C}](/latexrender/pictures/05b7eb94b0bd2edf15b2803031ddfe53.png)
![2\sqrt[]{5} = \sqrt[]{{1}^{2} + {4}^{2} -C} 2\sqrt[]{5} = \sqrt[]{{1}^{2} + {4}^{2} -C}](/latexrender/pictures/bca4b6ebecfa5a6851cf23574b0afeff.png) mas fiquei por ai.... minha dúvida é, nesse caso as coordenadas A e B correspondem a mesma circunferência, ou cada coordenada corresponde a uma respectiva equação? E, para encontrarmos a equação da circunferência realmente precisamos de 2 coordenadas?
mas fiquei por ai.... minha dúvida é, nesse caso as coordenadas A e B correspondem a mesma circunferência, ou cada coordenada corresponde a uma respectiva equação? E, para encontrarmos a equação da circunferência realmente precisamos de 2 coordenadas?
Grato desde já pela compreenção...
-
shirata
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 05, 2009 11:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Lucio Carvalho » Qui Nov 12, 2009 09:34
por Lucio Carvalho » Qui Nov 12, 2009 09:34
Olá shirata,
Tentarei explicar o exercício.
Primeiramente devemos lembrar que a equação geral da circunferência é:
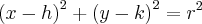
Onde (h, k) é a coordenada do centro da circunferência.
Então, com a ajuda dos dados, construímos o seguinte sistema de duas equações:
![{(1-h)}^{2}+{(4-k)}^{2}={(2\sqrt[]{5})}^{2} {(1-h)}^{2}+{(4-k)}^{2}={(2\sqrt[]{5})}^{2}](/latexrender/pictures/c7e53ae54b58a205c87f19e47d017147.png)
![{(7-h)}^{2}+{(-2-k)}^{2}={(2\sqrt[]{5})}^{2} {(7-h)}^{2}+{(-2-k)}^{2}={(2\sqrt[]{5})}^{2}](/latexrender/pictures/71251947c4190b39e4b95692fa904478.png)
-------------------------------------------------------------
Em seguida, resolvemos o sistema:
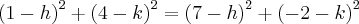
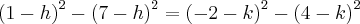



Quer dizer que existem infinitas circunferências que passam por A e B e tem o raio de
![2\sqrt[]{5} 2\sqrt[]{5}](/latexrender/pictures/8afe59aad7560ad383eefaf7fd49cdb9.png)
Para. por exemplo k = 0 temos h = 3
Assim, vamos escrever a equação de uma das circunferências:
![{(x-3)}^{2}+{(y-0)}^{2}={(2\sqrt[]{5})}^{2} {(x-3)}^{2}+{(y-0)}^{2}={(2\sqrt[]{5})}^{2}](/latexrender/pictures/9a8e30f9c7765893990a178e8f1135c9.png)
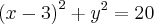
Espero ter ajudado e até breve!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por shirata » Dom Nov 15, 2009 09:25
por shirata » Dom Nov 15, 2009 09:25
valew kra!
deu pra entende sim, mas eu vo ve se faço mais alguns exercícios.
-
shirata
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 05, 2009 11:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Analítica
por maysa » Ter Abr 14, 2009 10:35
- 1 Respostas
- 7688 Exibições
- Última mensagem por Marcampucio

Ter Abr 14, 2009 15:52
Geometria Analítica
-
- GEOMETRIA ANALITICA
por GABRIELA » Ter Set 29, 2009 17:20
- 3 Respostas
- 5449 Exibições
- Última mensagem por GABRIELA

Qua Set 30, 2009 16:49
Geometria Analítica
-
- geometria analitica
por Jaison Werner » Sex Abr 23, 2010 21:19
- 3 Respostas
- 3949 Exibições
- Última mensagem por MarceloFantini

Dom Jun 13, 2010 19:03
Geometria Analítica
-
- geometria analitica
por Jaison Werner » Qui Abr 29, 2010 20:44
- 1 Respostas
- 2790 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 21:10
Geometria Analítica
-
- geometria analitica
por Jaison Werner » Qui Abr 29, 2010 20:50
- 1 Respostas
- 1526 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 21:15
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![2\sqrt[]{5} 2\sqrt[]{5}](/latexrender/pictures/8afe59aad7560ad383eefaf7fd49cdb9.png) .
.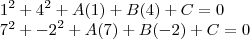
![R = \sqrt[]{{x}^{2} + {y}^{2} -C} R = \sqrt[]{{x}^{2} + {y}^{2} -C}](/latexrender/pictures/05b7eb94b0bd2edf15b2803031ddfe53.png)
![2\sqrt[]{5} = \sqrt[]{{1}^{2} + {4}^{2} -C} 2\sqrt[]{5} = \sqrt[]{{1}^{2} + {4}^{2} -C}](/latexrender/pictures/bca4b6ebecfa5a6851cf23574b0afeff.png)


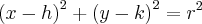
![{(1-h)}^{2}+{(4-k)}^{2}={(2\sqrt[]{5})}^{2} {(1-h)}^{2}+{(4-k)}^{2}={(2\sqrt[]{5})}^{2}](/latexrender/pictures/c7e53ae54b58a205c87f19e47d017147.png)
![{(7-h)}^{2}+{(-2-k)}^{2}={(2\sqrt[]{5})}^{2} {(7-h)}^{2}+{(-2-k)}^{2}={(2\sqrt[]{5})}^{2}](/latexrender/pictures/71251947c4190b39e4b95692fa904478.png)
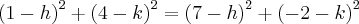
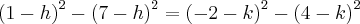



![{(x-3)}^{2}+{(y-0)}^{2}={(2\sqrt[]{5})}^{2} {(x-3)}^{2}+{(y-0)}^{2}={(2\sqrt[]{5})}^{2}](/latexrender/pictures/9a8e30f9c7765893990a178e8f1135c9.png)